Cho cấp số cộng ( u n ) có số hạng đầu u 1 = 3 và công sai d=2. Giá trị của u 7 bằng
A. 15
B. 17
C .19
D. 13
Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77
Cho cấp số cộng ( u n ) có số hạng đầu u 1 = 3 và công sai d = 2 . Giá trị của u 7 bằng:
A. 15
B. 17
C. 19
D. 13
Chọn đáp án A
Phương pháp
Sử dụng công thức SHTQ của cấp số cộng
u n = u 1 + ( n - 1 ) d
Cách giải
Ta có: u 7 = u 1 + 6 d = 15
Cho cấp số cộng u n có số hạng đầu u 1 = 2 và công sai d = 5. Giá trị của u 4 bằng
A. 22
B. 17
C. 12
D. 250
Cho cấp số cộng (un) có số hạng đầu u1 = 2 và công sai d = 5. Giá trị của u4 bằng
A. 22
B. 17
C. 12
D. 250
Cho cấp số cộng u n có số hạng đầu u 1 = 2 và công sai d = 5. Giá trị của u 4 bằng
A. 22
B. 17
C. 12
D. 250
Cho cấp số cộng u n có số hạng đầu u 1 = 2 và công sai d=5.Giá trị của S 4 bằng.
A. 17
B. 34
C. 19
D. 38
Cho cấp số cộng ( u n ) có số hạng đầu u 1 = 2 và công sai d = 5. Giá trị của u 4 bằng
A. 22
B. 17
C. 12
D. 250
Chọn đáp án B
Có u n = u 1 + ( n - 1 ) d = 5 n - 3
Khi đó u 4 = 17
Cho cấp số cộng (un) có công sai d = -3 và u22 + u32 + u42 đạt giá trị nhỏ nhất. Tính tổng S100 của số hạng đầu tiên của cấp số cộng đó.
A. S100 = -14650.
B. S100 = -14400.
C. S100 = -14250.
D. S100 = -15450.
Chọn C.
Đặt a = u1 thì u22 + u32 + u42 = (a + d)2 + (a + 2d)2 + (a + 3d2 = 3a2 – 36a + 126 = 3(a – 6)2 + 18 ≥ 18 với mọi a.
Dấu bằng xảy ra khi a – 6 = 0 hay a = 6.
Suy ra 6 = u1.
Ta có 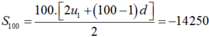
Cho cấp số cộng u n với số hạng đầu là u 1 = − 2017 và công sai d = 3. Bắt đầu từ số hạng nào trở đi mà các số hạng của cấp số cộng đều nhận giá trị dương?
A. u 674
B. u 672
C. u 675
D. u 673
Đáp án A
Công thức số hạng tổng quát là: u n = u 1 + n − 1 d = − 2017 + n − 1 .3 = 3 n − 2020.
Ta có: u n > 0 ⇔ 3 n − 2020 > 0 ⇔ n > 2020 3 ~ 673 , 3 ⇒ Bắt đầu từ số hạng u 674 các số hạng của cấp số cộng đều nhận giá trị dương.