Cho π < α 3π/2. Xác định dấu của các giá trị lượng giác sau cos(α - π/2)
PB
Những câu hỏi liên quan
Cho π < α 3π/2. Xác định dấu của các giá trị lượng giác sau sin(π/2 + α)
3π/2 < π/2 + α < 2π nên sin(π/2 + α) < 0
Đúng 0
Bình luận (0)
Cho π < α 3π/2. Xác định dấu của các giá trị lượng giác sau cot(α + π)
Cho π < α 3π/2. Xác định dấu của các giá trị lượng giác sau tan(3π/2 - α)
0 < 3π/2 - α < π/2 nên tan(3π/2 - α) > 0
Đúng 0
Bình luận (0)
Cho 0 < α < π/2. Xác định dấu của các giá trị lượng giác
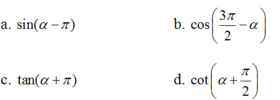
Vì 0 < α < π/2 nên sin α > 0, cos α > 0, tan α > 0, cot α > 0.
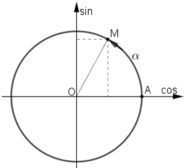
Cách 1: Dựa vào mối quan hệ giữa các giá trị lượng giác của các cung có liên quan đặc biệt
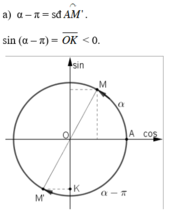
a) sin (α – π) = - sin (π – α) (Áp dụng công thức sin (- α) = - sin α)
= -sin α (Áp dụng công thức sin (π – α) = sin α)
Mà sin α > 0 nên sin (α – π) < 0.
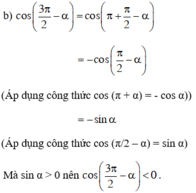
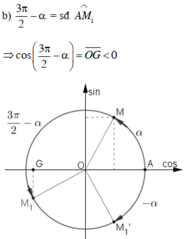
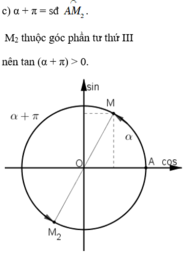
c) tan (α + π) = tan α.
Mà tan α > 0 nên tan (α + π) > 0.
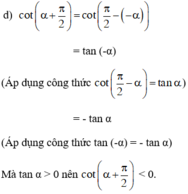
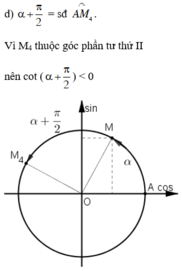
Cách 2: Dựa vào biểu diễn cung trên đường tròn lượng giác:
Vì 0 < α < π/2 nên ta biểu diễn α = sđ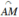 
như trên hình vẽ.
Đúng 0
Bình luận (0)
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM α, π α 3π/2, A(1; 0). Gọi
M
2
là điểm đối xứng với M qua trục Ox. Số đo của cung A
M
2
là A. α - π + k2π, k ∈ Z B. π - α + k2π, k ∈ Z C. 2π - α + k2π, k ∈ Z D. 3π/2 - α + k2π, k ∈ Z
Đọc tiếp
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π < α < 3π/2, A(1; 0). Gọi M 2 là điểm đối xứng với M qua trục Ox. Số đo của cung A M 2 là
A. α - π + k2π, k ∈ Z B. π - α + k2π, k ∈ Z
C. 2π - α + k2π, k ∈ Z D. 3π/2 - α + k2π, k ∈ Z
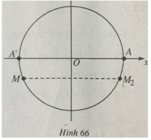
(h.66) Ta có
A M 2 = MA’ = MA + AA’
Suy ra
Sđ A M 2 = -α + π + k2π, k ∈ Z.
Vậy đáp án là B.
6.13. (h.67) Ta có
Sđ A M 3 = -sđ AM = -α + k2π, k ∈ Z.
Đáp án: D
Đúng 0
Bình luận (0)
Biểu thức tan(3π/2−α)+cot(3π−α)−cos(π/2−α)+2sin(π+α) sau khi thu gọn là gì?
Online chờ gấp, đa tạ các vị!
\(tan\left(\dfrac{3\pi}{2}-\alpha\right)+cot\left(3\pi-\alpha\right)-cos\left(\dfrac{\pi}{2}-\alpha\right)+2.sin\left(\pi+\alpha\right)\)
\(=tan\left(\pi+\dfrac{\pi}{2}-\alpha\right)+cot\left(-\alpha\right)-sin\alpha+2\left(sin\pi.cos\alpha+cos\pi.sin\alpha\right)\)
\(=tan\left(\dfrac{\pi}{2}-\alpha\right)-cot\alpha-sin\alpha+2.-sin\alpha\)
\(=cot\alpha-cot\alpha-3sin\alpha\)
\(=-3sin\alpha\)
Đúng 2
Bình luận (0)
H24
trang 40 SGK Toán 11 tập 1 - Kết nối tri thức
15 tháng 7 2023 lúc 12:46
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
a: pi/2<a<pi
=>sin a>0
\(sina=\sqrt{1-\left(-\dfrac{1}{\sqrt{3}}\right)^2}=\dfrac{\sqrt{2}}{\sqrt{3}}\)
\(sin\left(a+\dfrac{pi}{6}\right)=sina\cdot cos\left(\dfrac{pi}{6}\right)+sin\left(\dfrac{pi}{6}\right)\cdot cosa\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{\sqrt{3}}+\dfrac{1}{2}\cdot-\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{6}-2}{2\sqrt{3}}\)
b: \(cos\left(a+\dfrac{pi}{6}\right)=cosa\cdot cos\left(\dfrac{pi}{6}\right)-sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)
c: \(sin\left(a-\dfrac{pi}{3}\right)\)
\(=sina\cdot cos\left(\dfrac{pi}{3}\right)-cosa\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{2}+\sqrt{3}}{2\sqrt{3}}\)
d: \(cos\left(a-\dfrac{pi}{6}\right)\)
\(=cosa\cdot cos\left(\dfrac{pi}{6}\right)+sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}+\sqrt{2}}{2\sqrt{3}}\)
Đúng 0
Bình luận (0)
Cho sinα=3/5 và 0<α<π/2. Khi đó, giá trị của A= sin(π−α)+cos(π+α)+cos(−α) là gì?
Online chờ gấp, đa tạ các vị!
`A=sin(π-α)+cos(π+α)+cos(-α)`
`= sinα-cosα+cosα=sinα=3/5`
Đúng 2
Bình luận (0)
Rút gọn biểu thức
\(E = cot(5π+α).cos(α-\dfrac{3π}{2})+cos(α-2π)-2.cos(\dfrac{π}{2}+α)\)\(D = sin(π+α)-cos(\dfrac{π}{2}-α)+cot(4π-α)+tan(\dfrac{5π}{2}-α)\)