Xét tính tăng, giảm của các dãy số u n , biết: u n = n - 1 n + 1
PB
Những câu hỏi liên quan
Xét tính tăng, giảm và bị chặn của các dãy số u n , biết: u n = n + 1 - n
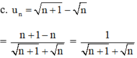
+ Xét tính tăng giảm.
Với mọi n ∈ N ta có:
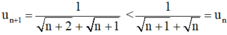
⇒ un + 1 < un với mọi n ∈ N.
⇒ (un) là dãy số giảm.
+ Xét tính bị chặn.
un > 0 với mọi n.
⇒ (un) bị chặn dưới.
un ≤ u1 = √2 - 1 với mọi n
⇒ (un) bị chặn trên.
⇒ (un) bị chặn.
Đúng 0
Bình luận (0)
Xét tính tăng , giảm của các dãy số \(\left(u_n\right)\) biết
\(u_n=\sqrt{n+3}-\sqrt{n}\)
Lời giải:
Có:
\(u_{n+1}-u_n=\sqrt{n+4}-\sqrt{n+1}-(\sqrt{n+3}-\sqrt{n})\)
\(=(\sqrt{n+4}-\sqrt{n+3})-(\sqrt{n+1}-\sqrt{n})\)
\(=\frac{1}{\sqrt{n+4}+\sqrt{n+3}}-\frac{1}{\sqrt{n+1}+\sqrt{n}}<0\) với mọi $n\in\mathbb{N}^*$
$\Rightarrow u_{n+1}< u_n$ với mọi $n\in\mathbb{N}^*$
Do đó dãy đã cho là dãy giảm.
Đúng 1
Bình luận (0)
Xét tính tăng , giảm của các dãy số \(\left(u_n\right)\) biết
\(u_n=\dfrac{\sqrt{n+11}}{n}\)
Lời giải:
Thấy rằng $u_n>0$ với mọi $n\in\mathbb{N}^*$
\(\frac{u_{n+1}}{u_n}=\frac{\sqrt{n+12}}{n+1}: \frac{\sqrt{n+11}}{n}=\frac{\sqrt{n^2(n+12)}}{\sqrt{(n+1)^2(n+11)}}=\sqrt{\frac{n^3+12n^2}{n^3+13n^2+23n+11}}<1\) với mọi $n\in\mathbb{N}^*$
$\Rightarrow u_{n+1}< u_n$ với mọi $n\in\mathbb{N}^*$
$\Rightarrow (u_n)$ là dãy giảm.
Đúng 1
Bình luận (0)
Xét tính tăng, giảm và bị chặn của các dãy số u n , biết: u n = n + 1 n
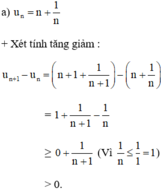
⇒ un + 1 > un với mọi n ∈ N
⇒ (un) là dãy tăng.
+ Xét tính bị chặn:
(un) là dãy tăng
⇒ u1 = 2 < u2 < u3 < …< un ∀n ∈ N*
⇒ un ≥ 2 ∀n ∈ N*
⇒ (un) bị chặn dưới.
(un) không bị chặn trên.
⇒ un không bị chặn.
Đúng 0
Bình luận (0)
Xét tính tăng , giảm của các dãy số \(\left(u_n\right)\) biết
\(u_n=\dfrac{\left(-1\right)^n}{n+2}\)
Lời giải:
Với $n$ lẻ bất kỳ:
$u_n<0; u_{n+1>0; u_{n+2}< 0$
$\Rightarrow u_n< u_{n+1}> u_{n+2}$ với mọi $n$ lẻ bất kỳ
Do đó dãy không tăng cũng không giảm.
Đúng 1
Bình luận (0)
xét tính tăng, giảm của các dãy số sau
\(u_n=\dfrac{n+2}{n}\)
\(u_n=\dfrac{n+2}{n}\)
\(u_{n+1}=\dfrac{n+3}{n+1}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{n+3}{n+1}-\dfrac{n+2}{n}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{n\left(n+3\right)-\left(n+1\right)\left(n+2\right)}{n\left(n+1\right)}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{n^2+3n-\left(n^2+3n+2\right)}{n\left(n+1\right)}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{n^2+3n-n^2-3n-2}{n\left(n+1\right)}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{-2}{n\left(n+1\right)}< 0\)
Vậy dãy số \(u_n\) đã cho là dãy giảm
Đúng 1
Bình luận (0)
Xét tính tăng , giảm của các dãy số \(\left(u_n\right)\) biết :
\(a,u_n=\dfrac{\sqrt{n+11}}{n}\)
\(b,u_n=\dfrac{4^n-1}{4^n+5}\)
Xét tính tăng , giảm của các dãy số \(\left(u_n\right)\) biết :
\(a,u_n=\dfrac{\left(-1\right)^n}{n+2}\)
\(b,u_n=\sqrt{n+3}-\sqrt{n}\)
Xét tính tăng , giảm của các dãy số \(\left(u_n\right)\) biết :
\(a,u_n=\dfrac{\sqrt{n+11}}{n}\)
\(b,u_n=\dfrac{4^n-1}{4^n+5}\)


