Phương trình x − 512 + 1024 − x = 16 + 4 x − 512 1024 − x 8 có bao nhiêu nghiệm?
A. 4 nghiệm
B. 2 nghiệm
C. 3 nghiệm
D. 8 nghiệm
Phương trình x − 512 + 1024 − x = 16 + 4 x − 512 1024 − x 8 có bao nhiêu nghiệm?
A. 2 nghiệm
B. 8 nghiệm
C. 4 nghiệm
D. 3 nghiệm
Đáp án D
Lời giải:
Đặt t = x − 512 1024 − x 8 ≥ 0 , ta có
t 4 = x − 512 1024 − x ≤ x − 512 + 1024 − x 2 = 256 ⇒ 0 ≤ t ≤ 4
Với t = 4 thì ta tìm được 1 giá trị của x = 768
Với 0 ≤ t ≤ 4 thì ta tìm được 2 giá trị của x (Khi đó phương trình của Định lý Viét đảo có 2 nghiệm phân biệt)
Bình phương 2 vế phương trình đã cho, ta được
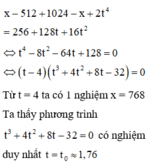
(sử dụng máy tính).
Từ đó ta có 2 nghiệm x thỏa mãn
Do đó phương trình đã cho có 3 nghiệm.
Phương trình x - 512 + 1024 - x = 16 + 4 x - 512 1024 - x 8 có bao nhiêu nghiệm?
A. 4.
B. 2.
C. 3.
D. 8.
Phương trình x - 512 + 1024 - x = 16 + 4 x - 512 1024 - x 8 có bao nhiêu nghiệm?
A. 4 nghiệm
B. 2 nghiệm
C. 3 nghiệm
D. 8 nghiệm
Đáp án C
x - 512 + 1024 - x = 16 + 4 x - 512 1024 - x 8 (*), 512 ≤ x ≤ 1024
t = x - 512 1024 - x 8 ⇒ t 4 = x - 512 1024 - x ≤ x - 512 + 1024 - x 2 = 256 ⇒ 0 ≤ t ≤ 4 t = 4 ⇒ x = 768 0 ≤ t ≤ 4
=> Bình phương hai vế (*):
( t - 4 ) t 3 + 4 t 2 + 8 t - 32 = 0 ⇔ [ x ≈ 512 , 18 x ≈ 1023 , 82
1.<,>,= ?
256 x 6.....512 x 3
512 x 3.....256 x 6
999 x 2.....1000
512 x 5.....1024
1024.....512 x 5
1024.....512 x 2
512.....256 x 2
256.....128 x 2
128.....64 x 2
64.....32 x 2
32.....16 x 2
256 x 6=512 x 3
512 x 3=256 x 6
999 x 2>1000
512 x 5>1024
1024<512 x 5
1024=512 x 2
512=256 x 2
256=128 x 2
128=64 x 2
64=32 x 2
32=16 x 2
Giải các phương trình:
a) 3 x 4 − 2 x + 7 6 ≥ 1 − x + 1 2 ;
b) x + 2 x − 5 4 − x 2 + 1 3 > 5 − x 2 − 5 12
Giải các bất phương trình và biểu diễn nghiệm trên trục số:
a ) x + 2 2 - 10 ≥ x + 3 x + 2 - 4 b ) x - 2 18 - 2 x + 5 12 > x + 6 9 - x - 3 6
a)
⇔ x2 + 6x + 9 – 10 ≥ x2 + 3x + 2x + 6 – 4
⇔ x2 – x2 + 6x – 3x – 2x ≥ –9 + 10 + 6 – 4
⇔ x ≥ 3
Tập nghiệm: S = {x | x ≥ 3}.
Biểu diễn trên trục số:
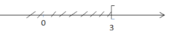
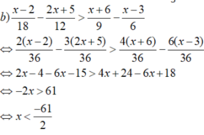
Vậy tập nghiệm của bất phương trình là
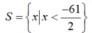
lam vay co duoc ko
1/2+1/4+1/8+... +1/512+1/1024=1-1/2+1/2-1/4+...+1/512-1/1024=1-1/1024=1/1023
kết quả sai rồi phải là \(\frac{1023}{1024}\)
làm vậy cũng dc nhưng kết quả phải là \(\frac{1023}{1024}\) hén
Tính biểu thức sau một cách hợp lí nhất:
a,1998 x 1996 + 1997 x 11 + 1985/1997 x 1996 - 1995 x 19961
b,A=1/2+1/4+1/8+......+1/512+1/1024
1/2+1/4+1/8+1/16+...+1/512+1/1024
trình bày bài giải ra nha ai đúng và nhanh nhất sẽ đc tick
Đặt tổng trên là A . Ta có:
\(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{1024}\)
\(2A=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{1024}\)
\(2A-A=\left(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{1024}\right)-\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{1024}\right)\)
\(A=1-\frac{1}{1024}\)
\(A=\frac{1023}{1024}\)