Số 1458 là số hạng thứ bao nhiêu của cấp số nhân u n có số hạng đầu u 1 = 2 và công bội q = 3
A. 8
B. 5
C. 6
D. 7
Số 1458 là số hạng thứ bao nhiêu của cấp số nhân (un) có công bội u1=2 và q=3
A. 8
B. 5
C. 6
D. 7
Số 1458 là số hạng thứ bao nhiêu của cấp số nhân ( u n ) có công bội u 1 = 2 v à q = 3
A. 8
B. 5
C. 6
D. 7
Phương pháp:
Cấp số nhân ( u n ) có số hạng đầu u 1 và công bội q thì có số hạng thứ n là
![]()
Cách giải:
Gọi số hạng thứ n là u n = 1458
⇔ 2 . 3 n - 1 = 1458
⇔ 3 n - 1 = 729 ⇔ n - 1 = 6 ⇔ n = 7
Chọn: D
Ba số có tổng là 217 có thể coi là các số hạng liên tiếp của một cấp số nhân, hoặc là các số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Hỏi phải lấy bao nhiêu số hạng đầu của cấp số cộng để tổng của chúng là 820?
Ba số có tổng là 217 có thể coi là các số hạng liên tiếp của một cấp số nhân, hoặc là các số hạng thứ hai, thứ 9 và thứ 44 của một cấp số cộng. Hỏi phải lấy bao nhiêu số hạng đầu của cấp số cộng để tổng của chúng là 820 ?
Gọi ba số đó là \(x,y,z\). Do ba số là các số hạng thứ hai, thứ 9 và thứ 44 của một cấp số cộng nên:
\(x;y=x+7d;z=x+42d\). (Với d là công sai của cấp số cộng).
Ta có: \(x+y+z=x+x+7d+x+42d=3x+49d=217\).
Mặt khác x, y, z là các số hạng liên tiếp của một cấp số nhân nên:
\(y^2=xz\)\(\Leftrightarrow\left(x+7d\right)^2=x\left(x+42d\right)\)\(\Leftrightarrow-28xd+49d^2=0\)\(\Leftrightarrow7d\left(-4x+7d\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}d=0\\-4x+7d=0\end{matrix}\right.\).
Với \(d=0\) suy ra \(x=y=z=\dfrac{217}{3}\).
Suy ra: \(n=820:\dfrac{217}{3}=\dfrac{2460}{217}\notin N\).
Với \(4+7d=0\). Ta có hệ:
\(\left\{{}\begin{matrix}4x+7d=0\\3x+49d=217\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=7\\d=4\end{matrix}\right.\).
Vậy \(u_1=7-4=3\).
Có \(S_n=\dfrac{\left[2u_1+\left(n-1\right)d\right]n}{2}=\dfrac{\left[2.3+\left(n-1\right)4\right]n}{2}=820\)
\(\Rightarrow n=20\left(tm\right)\).
Cho cấp số nhân \(\left( {{u_n}} \right)\) với số hạng đầu \({u_1} = - 5\), công bội q = 2
a) Tìm \({u_9}\)
b) Số \( - 320\) là số hạng thứ bao nhiêu của cấp số nhân?
c) Số 160 có phải là một số hạng của cấp số nhân trên không?
a) \({u_9} = {u_1}.{q^{9 - 1}} = \left( { - 5} \right){.2^8} = - 1280\)
b) Ta có: \( - 320 = \left( { - 5} \right){.2^{n - 1}} \Leftrightarrow {2^{n - 1}} = 64 \Leftrightarrow n = 7\)
\( - 320\) là số hạng thứ 7 của cấp số nhân
c) Ta có: \(160 = \left( { - 5} \right){.2^{n - 1}} \Leftrightarrow {2^{n - 1}} = - {2^5}\)
160 không là số hạng của cấp số nhân
Cho cấp số nhân có số hạng đầu bằng 1, công bội bằng 3. Hỏi số hạng thứ 2018 của cấp số đó là một số tự nhiên có bao nhiêu chữ số?
Cấp số nhân ( u n ) có u 1 + u 5 = 51 u 2 + u 6 = 102
a) Tìm số hạng đầu và công bội của cấp số nhân:
b) Hỏi tổng của bao nhiêu số hạngđầu tiên sẽ bằng 3096?
c) Số 12288 là số hạng thứ mấy?
a ) u 1 = 3 , q = 2 b ) n = 10 c ) n = 13
Ba số phân biệt có tổng 217, là các số hạng liên tiếp của một cấp số nhân, theo thứ tự đó chúng lần lượt là số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Biết tổng của n số hạng đầu tiên của cấp số cộng là 820, khi đó n bằng
A. 21
B. 42
C. 20
D. 17
Chọn C
Gọi ba số đó lần lượt là x,y,z
Do ba số là các số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng nên ta có liên hệ: y = x + 7 d , z = x + 42 (với d là công sai của cấp số cộng)
Theo giả thiết ta có: x + y + z = x + x + 7 d + x + 42 d = 3 x + 49 d = 217
Mặt khác do x,y,z là các số hạng liên tiếp của một cấp số nhân nên
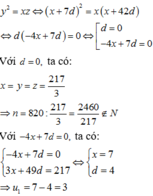
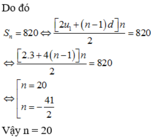
Ba số phân biệt có tổng 217, là các số hạng liên tiếp của một cấp số nhân, theo thứ tự đó chúng lần lượt là số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Biết tổng của n số hạng đầu tiên của cấp số cộng là 820, khi đó n bằng
A. 21
B. 42
C.20
D. 17