Gọi S là diện tích hình phẳng giới hạn bởi các đường y = e x , y = 0 , x = 0 , x = 2 Mệnh đề nào dưới đây đúng?
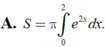
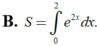
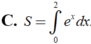
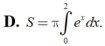
Gọi S là diện tích hình phẳng giới hạn bởi các đường y = l x , y = 0 , x = 0 , x = 2 Mệnh đề nào dưới đây đúng?
A. S = π ∫ 0 2 l 2 x d x
B. S = ∫ 0 2 l 2 x d x
C. S = ∫ 0 2 l x d x
D. S = π ∫ 0 2 l x d x
Chọn C
Diện tích hình phẳng giới hạn bởi các đường y = l x , y = 0 , x = 0 , x = 2 được tính theo công thức S = ∫ 0 2 l x d x = ∫ 0 2 l x d x
Gọi S là diện tích của hình phẳng giới hạn bởi các đường y = 3 x , y = 0 , x = 0 , x = 2 . Mệnh đề nào dưới đây đúng?
A. S = ∫ 0 2 3 x d x
B. S = π ∫ 0 2 3 2 x d x
C. S = π ∫ 0 2 3 x d x
D. ∫ 0 2 3 2 x d x
Gọi S là diện tích hình phẳng giới hạn bởi các đường y = x 3 , y = 2 - x , y = 0 . Mệnh để nào sau đây là đúng?
A. S = ∫ 0 1 x 3 d x + ∫ 1 2 x - 2 d x
B. S = ∫ 0 2 x 3 + x - 2 d x
C. S = 1 2 + ∫ 0 1 x 3 d x
D. S = ∫ 0 2 x 3 + x - 2 d x
Diện tích hình phẳng giới hạn bởi các đường y = 1 + ln x x , y = 0 , x = 1 và x = e là S = a 2 + b . Khi đó giá trị a 2 + b 2 là:
A. 2 3 .
B. 4 3 .
C. 20 9 .
D.2
Đáp án C
Ta có S = ∫ 1 e 1 + ln x x d x . Đặt 1 + ln x = t ⇒ ln x = t 2 − 1 ⇒ 1 x = d x = 2 t d t
Đổi cận: x = 1 ⇒ t = 1 ; x = e ⇒ t = 2
⇒ S = ∫ 1 2 t .2 t d t = 2 t 3 3 2 1 = 4 2 3 − 2 3 = 4 2 − 2 3 ⇒ a = 4 3 b = − 2 3
⇒ a 2 + b 2 = 16 9 + 4 9 = 20 9
Diện tích hình phẳng giới hạn bởi các đường y = 1 + ln x x , y=0, x=1 và x=e là S = a 2 + b . Khi đó giá trị a 2 + b 2 là:
A. 2 3
B. 4 3
C. 20 9
D. 2
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x),y=0,x=0,x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0,x=a bằng
A. S/4.
B. 4S.
C. 2S.
D. S/2.
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x), y=0, x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0, x=a bằng:
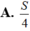
![]()
![]()
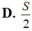
Tính diện tích S của hình phẳng giới hạn bởi các đường y = e x , y = e - x , x = 1 .
A. S = e + 1 2 - 2
B. S = e - 1 e - 2
C. S = e + 1 e
D. S = e + 1 e - 2
Tính diện tích S của hình phẳng giới hạn bởi các đường y = ex, y = e–x, x = 1.
A. S = e + 1 2 - 2
B. S = e - 1 e - 2
C. S = e + 1 e
D. S = e + 1 e - 2