Cho số phức z = a + b i a , b ∈ ℝ . Môdun của z được tính theo công thức nào sau đây?
A. |z| = a + b
B. z = a 2 + b 2
C. z = a − b
D. z = a 2 + b 2
Cho số phức z = a + bi (a,b ∈ ℝ ) thỏa mãn z - 1 z - i v à z - 3 i z + i . Tính P = a + b.
A. P = 7
B. P = -1
C. P = 1
D. P = 2
Cho số phức z = a + b i a , b ∈ ℝ thỏa mãn z + 2 + i − z 1 + i = 0 , z > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7
Đáp án D
z + 2 + i − z ( 1 + i ) = 0 ⇔ ( a + b i ) + 2 + i − a 2 + b 2 ( 1 + i ) = 0 ⇔ a + 2 − a 2 + b 2 + ( b + 1 − a 2 + b 2 ) i = 0 ⇒ a + 2 − a 2 + b 2 = 0 b + 1 − a 2 + b 2 = 0 ⇒ a − b + 1 = 0 ⇒ a = b − 1 ⇒ b + 1 − ( b − 1 ) 2 + b 2 = 0 ⇒ 2 b 2 − 2 b + 1 = b + 1 ⇒ b ≥ − 1 b 2 − 4 b = 0 ⇒ b = 0 b = 4 ⇒ a = − 1 ( L ) a = 3 ⇒ P = 4 + 3 = 7
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(1+i) = 0 và |z| > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7
Đáp án D.
Đặt z = a + bi => a + bi ![]()
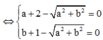
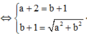
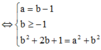

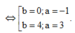
Do |z| > 1 => a = 3, b = 4
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(i+1) = 0 và |z| > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(1+i) = 0 và |z| > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7
Cho số phức z = a + b i ( a , b ∈ ℝ ) thỏa mãn z - 1 z - i = 1 và z - 3 i z + i = 1 .Tính P=a+b.
A. P=7
B. P=-1
C. P=1
D. P=2
Cho số phức z = a + b i a , b ∈ ℝ thỏa mãn z + 2 + i − z 1 + i = 0 và z > 1. Tính P = a + b .
A. P = − 1.
B. P = − 5.
C. P = 3.
D. P = 7.
Đáp án D.
Đặt
z = a + b i ⇒ a + b i + 2 + i − a 2 + b 2 1 + i = 0
⇔ a + 2 − a 2 + b 2 = 0 b + 1 − a 2 + b 2 = 0 ⇔ a + 2 = b + 1 b + 1 = a 2 + b 2 ⇔ a = b − 1 b ≥ − 1 b 2 + 2 b + 1 = a 2 + b 2 ⇔ a = b − 1 b ≥ − 1 2 b + 1 = b − 1 2 ⇔ b = 0 ; a = − 1 b = 4 ; a = 3 .
Do z > 1 ⇒ a = 3 , b = 4.
Cho số phức z = a + b i a , b ∈ ℝ thỏa mãn z − 1 z − i = 1 và z − 3 i z + i = 1 . Tính P = a + b.
A. P = 7
B. P = -1
C. P = 1
D. P = 2
Trong mặt phẳng phức, gọi M là điểm biểu diễn cho số phức ( z - z ¯ ) 2 với z = a + b i ( a , b ∈ ℝ , b ≠ 0 )
Chọn kết luận đúng
A. M thuộc tia Ox.
B. M thuộc tia Oy
C. M thuộc tia đối của tia Ox.
D. M thuộc tia đối của tia Oy.
Đáp án C
Phương pháp.
Tính trực tiếp ![]()
Lời giải chi tiết.
Ta có

Do ![]()
Do đó M có phần thực âm, phần ảo bằng 0, nên thuộc tia đối của tia Ox.
Trong mặt phẳng phức, gọi M là điểm biểu diễn cho số phức ( z - z ¯ ) 2 v ớ i z = a + b i ( a , b ∈ ℝ , b ≠ 0 ) . Chọng kết luận đúng.
![]()
![]()
![]()
![]()