Cho hình chóp S.ABCD có đá ABCD là hình thoi cạnh 2a, A C = 3 a là tam giác đều, S A = 120 ° . Tính thể tích khối chóp S.ABCD
A. 3 a 3
B. 3 3 a 3 2
C. 6 a 3
D. 2 3 a 3 3
Cho hình chóp S.ABCD có đá ABCD là hình thoi cạnh 2 a , A C = 3 a , S A B là tam giác đều, S A D ^ = 120 ° . Tính thể tích khối chóp S.ABCD
A. 3 a 3
B. 3 3 a 3 2
C. 6 a 3
D. 2 3 a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a, A C = a 3 , SAB là tam giác đều, S A D ^ = 120 ° . Tính thể tích của khối chóp S.ABCD
A. a 3 3
B. 3 a 3 3 2
C. a 3 6
D. 2 a 3 3 3
HD: Gọi H là tâm đường tròn ngoại tiếp ∆SBD

Bán kính đường tròn ngoại tiếp ∆SBD là

Bài 5. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên hợp với đáy một góc . Tính VS ABCD . theo a và . Bài 6. Tính thể tích khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc ASB = α . Áp dụng: Tính VS ABCD . trong trường hợp α = 60 độ.
Bài 7. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC =120độ . Cho SA vuông góc với đáy và SC = 2a .Tính thể tích hình chóp S.ABCD.
Bài 8. Cho hình chóp S.ABCD có đáy ABCD là một hình thang cân (AB//CD) với AC=20 cm BC=15 cm AB=25 cm . Cho SA vuông góc với đáy và SA =18cm . Tính thể tích của khối chóp.
Bài 9. Cho hình chóp S.ABC có SA vuông góc với đáy. Mặt bên SBC là tam giác đều cạnh a. Cho gócBAC =120 . Tính VS ABC .
. Bài 10. Cho khối chóp S.ABC có đường cao SA bằng a, đáy là tam giác vuông cân có AB= BC= a . Gọi B' là trung điểm của SB, C' là chân đường cao hạ từ A của tam giác S.ABC:
a.Tính thể tích khối chóp S.ABC
b.Chứng minh SC vuông góc với (AB'C')
c.Tính thể tích khối chóp S.ABC
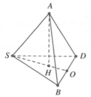
Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và tam giác ABD đều. SO vuông góc mặt phẳng (ABCD) và SO = 2a. M là trung điểm của SD. Tang góc giữa CM và (ABCD) là:
A. 4 13
B. 4 13 13
C. 13 4
D. 13 13
Chọn đáp án B.
Gọi I là trung điểm OD => MI là đường trung bình tam giác SOD
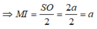 và MI//SO
và MI//SO ![]()
IC là hình chiếu của MC lên mặt phẳng (ABCD).
Góc giữa MC với (ABCD) là M C I ^
Tam giác ABD đều ![]()
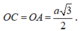
Xét tam giác OCI vuông tại O:
![]()
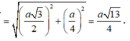
Xét tam giác CMI vuông tại I:
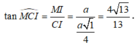
cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a, góc BAD=120. Mặt bên (SAB) có SA=a, SB= a\(\sqrt{3}\) và vuông góc với mặt phẳng đáy. Gọi G là trọng tâm tam giác SCD. Tính thể tích hình chóp SABCD và khoảng cách từ G đến mặt phẳng (SAB)
Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh 2a, tam giác SAB vuông cân tại S, tam giác SCD đều thì thể tích khối S.ABCD là:
A. 4 a 3 3 3
B. 4 a 3 3
C. 2 a 3 3
D. 2 a 3 3 3
Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và tma giác ABD đều. SO vuông góc mặt phẳng (ABCD) và SO=2a. M là trung điểm của SD. Tang góc giữa CM và (ABCD) là:
A. 4 13
B. 4 13 13
C. 13 4
D. 13 13
1. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a; SA = 2a và vuông góc với mặt phẳng đáy. Gọi H là trung điểm của SB, K là hình chiếu vuông góc của A lên SC. Tính thể tích khối chóp S.AHK.
2. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc BAD = 120 độ , SA ⊥ (ABCD). Biết rằng khoảng cách từ điểm A đến đường thẳng SC bằng \(\dfrac{a\sqrt{2}}{2}\). Tính thể tích của khối chóp S.ABCD.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, A B C ^ = 60 ° . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD.
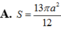
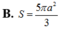
![]()
![]()