Cho a, b là các số thực thỏa mãn a > 0 v à a ≠ 1 biết phương trình a x - 1 a x = 2 c o s ( b x ) có 7 nghiệm thực phân biệt. Tìm số nghiệm thực phân biệt của phương trình a 2 x - 2 a x ( c o s b x + 2 ) + 1 = 0
A. 14
B. 0
C. 7
D. 28
cho phương trình ax^2+bx+c=0 với các số a,b,c là các số thực nghiệm khác 0 và thỏa mãn điều kiện a+b+2c=0. Chứng minh rằng phương trình trên luôn có nghiệm trên tập số thực
Đặt \(f\left(x\right)=ax^2+bx+c\).
\(f\left(0\right)=c;f\left(1\right)=a+b+c\)
Do \(a+b+2c=0\) nên c và \(a+b+c\) trái dấu. Suy ra f(0)f(1) < 0 nên f(x) = 0 luôn có ít nhất 1 nghiệm tren (0; 1).
Cho các số thực a,b,c thỏa mãn 4a+b>8+2b và a+b+c<-1. Khi đó phương trình x^3 + ax^2 + b^x + c = 0 có bao nhiêu nghiệm thực phân biệt?
giúp em với ạ
thôi để giải luôn
Xét phương trình: \(x^3+ax^2+bx+c=0\left(1\right)\)
Đặt : \(f\left(x\right)=x^3+2x^2+bc+c\)
Từ giả thiết \(\left\{{}\begin{matrix}4a+c>8+2b\Rightarrow-8+4a-2b+c>0\Rightarrow f\left(-2\right)>0\\a+b+c< -1\Rightarrow1+a+b+c< 0\Rightarrow f\left(1\right)< 0\end{matrix}\right.\)
Do đó \(f\left(-2\right).f\left(1\right)< 0\) nên pt (1) có ít nhất một nghiệm trong \(\left(-2;1\right)\)
Ta nhận thấy:
\(\overset{lim}{x\rightarrow-\infty}f\left(x\right)=-\infty\) mà \(f\left(-2\right)>0\) nên phương trình (1) có ít nhất một nghiệm \(\alpha\in\left(-\infty;-2\right)\)
Tương tự: \(\overset{lim}{x\rightarrow+\infty}f\left(x\right)=+\infty\) mà \(f\left(1\right)< 0\) nên phương trình (1) có ít nhất một nghiệm \(\beta\in\left(1+\infty\right)\)
Như vậy phương trình đã cho có ít nhất 3 nghiệm thực phân biệt, mặt khác phương trình bậc 3 có tối đa 3 nghiệm nên pt trên sẽ có 3 nghiệm thực phân biệt.
Cho các số thực a,b,c thỏa mãn 4a+b>8+2b và a+b+c<-1. Khi đó số nghiệm thực phân biệt của phương trình x 3 + a x 2 + b x + c = 0 bằng
A.0
B.3
C.2
D.1
Cho phương trình: x(x-2)-(x+3)^2 + 1=0 Nghiệm của phương trình thỏa mãn điều kiện nào sao đây?
A. Là một số tự nhiên.
B. Là phần tử của tập hợp A = [-1;1]
C. Là phần tử của tập hợp B=[0;2]
D. Là một số thực không âm.
Cho các số thực a,b,c thỏa mãn a+c>b+1 và 4a+2b+c<-8. Khi đó số nghiệm thực phân biệt của phương trình x 3 + a x 2 + b x + c = 0 bằng
A.0
B.3
C.2
D.1
cho a,b,c là các số thực thỏa mãn a/6 +b/5 +c/4 =0 .Chứng minh rằng phương trình ax^2+bx+c=0 luộn có nghiệm.
bn ngốc à,nếu vậy thì k cho mk đi
Cho phương trình 2 log 4 2 x 2 - x + 2 m - 4 m 2 + log 1 2 x 2 + m x - 2 m 2 = 0 . Biết rằng S = a ; b ∪ c ; d , a < b < c < d là tập hợp các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt x1, x2 thỏa mãn x 1 2 + x 2 2 > 1 . Tính giá trị biểu thức A = a + b + 5c + 2d.
A. A = 1
B. A = 2
C. A = 0
D. A = 3
Đáp án B
P T ⇔ log 2 2 x 2 - x + 2 m - 4 m 2 + log 2 x 2 + m x - 2 m 2 = 0
⇔ 2 x 2 - x + 2 m - 4 m 2 = x 2 + m x - 2 m 2 > 0
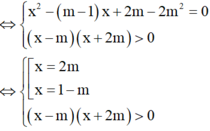
Điều kiện để pt đã cho có 2 nghiệm
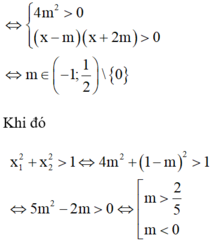
Do đó
S = - 1 ; 0 ∪ 2 5 ; 1 2 ⇒ A = - 1 + 2 + 1 = 2
Tập hợp tất cả các số thực x không thỏa mãn bất phương trình 9 x 2 - 4 + ( x 2 - 4 ) . 2019 x - 1 ≥ 1 là khoảng (a;b). Tính b-a
A. 5
B. -1
C. -5
D. 4
Cho a, b là các số thực dương thỏa mãn a + b = 1. Tìm giá trị nhỏ nhất của biểu thức P = a^2 + b^2 + 1/a + 1/b
Giải phương trình căn(x-1) + căn (3-x) =x^2-4x+6
Bài 1: Áp dụng BĐT Cauchy-Schwarz ta có:
\(\left(1^2+1^2\right)\left(a^2+b^2\right)\ge\left(a+b\right)^2\Rightarrow a^2+b^2\ge\frac{1}{2}\)
Lại có BĐT \(\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\Leftrightarrow\left(a-b\right)^2\ge0\)
\(\Rightarrow\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}=4\left(a+b=1\right)\)
Cộng theo vế 2 BĐT trên có:
\(P=a^2+b^2+\frac{1}{a}+\frac{1}{b}\ge4+\frac{1}{2}=\frac{9}{2}\)
Đẳng thức xảy ra khi \(a=b=\frac{1}{2}\)
Bài 2: Áp dụng BĐT AM-GM ta có:
\(VT^2=\left(x-1\right)+\left(3-x\right)+2\sqrt{\left(x-1\right)\left(3-x\right)}\)
\(=2+2\sqrt{\left(x-1\right)\left(3-x\right)}\)
\(\le2+\left(x-1\right)+\left(3-x\right)=4\)
\(\Rightarrow VT^2\le4\Rightarrow VT\le2\left(1\right)\). Lại có:
\(VP=x^2-4x+4+2=\left(x-2\right)^2+2\ge2\left(2\right)\)
Từ (1);(2) xảy ra khi
\(VT=VP=2\Rightarrow\left(x-2\right)^2+2=2\Rightarrow\left(x-2\right)^2=0\Rightarrow x=2\) (thỏa)
Vậy x=2 là nghiệm của pt
2. \(\sqrt{x-1}+\sqrt{3-x}=x^2-4x+6\)
Điều kiện : \(\hept{\begin{cases}x-1\ge0\\3-x\ge0\end{cases}\Leftrightarrow}1\le x\le3\left(1\right)\)
(Nháp nhé : dễ thấy phương trình có nghiệm \(x=2\) nên ta sẽ thêm bớt để có \(\left(x-2\right)\)là nhân tử chung )
\(\Leftrightarrow\sqrt{x-1}-1+\sqrt{3-x}-1=x^2-4x+4\)
nhân liên hợp có :
\(\Leftrightarrow\frac{\left(\sqrt{x-1}-1\right)\left(\sqrt{x-1}+1\right)}{\left(\sqrt{x-1}+1\right)}+\frac{\left(\sqrt{3-x}+1\right)\left(\sqrt{3-x}-1\right)}{\left(\sqrt{3-x}+1\right)}=\left(x-2\right)^2\)
\(\Leftrightarrow\frac{x-2}{\left(\sqrt{x-1}+1\right)}+\frac{-\left(x-2\right)}{\left(\sqrt{3-x}+1\right)}=\left(x-2\right)^2\)
\(\Leftrightarrow\left(x-2\right)\left[\frac{1}{\left(\sqrt{x-1}+1\right)}-\frac{1}{\left(\sqrt{3-x}+1\right)}-\left(x-2\right)\right]=0\)
\(x-2=0\Leftrightarrow x=2\)vì \(\left(\sqrt{x-1}+1\right)>\left(\sqrt{3-x}+1\right)\Rightarrow\frac{1}{\left(\sqrt{x-1}+1\right)}-\frac{1}{\left(\sqrt{3-x}+1\right)}< 0\)nên \(\frac{1}{\left(\sqrt{x-1}+1\right)}-\frac{1}{\left(\sqrt{3-x}+1\right)}-\left(x-2\right)< 0\forall x\in\left\{1.3\right\}\)do đó phương trình vô nghiệmKết luận nghiệm nhé