Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số y = x 2 - 4 , trục Ox, đường thẳng x=3. Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng (H) quanh trục hoành.
![]()
![]()
![]()
![]()
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số y = x 2 - 4 , trục Ox, đường thẳng x=3. Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng (H) quanh trục hoành
![]()
![]()
![]()
![]()
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số y = x 2 - 4 , trục Ox, đường thẳng x = 3 . Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng (H) quanh trục hoành
A. V = 7 π 3 (đvtt)
B. V = 5 π 3 (đvtt)
C. V = 2 π (đvtt)
D. V = 3 π (đvtt)
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y= x 4 - x 2 , trục Ox và đường thẳng x=1. Tính thể tích V của khối tròn xoay thu được khi quay hình H xung quanh trục Ox
A. V = π 2 ln 4 3
B. V = 1 2 ln 4 3
C. V = π 2 ln 3 4
D. V = π ln 4 3
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y = x 4 − x 2 , trục Ox và đường thẳng x = 1. Tính thể tích V của khối tròn xoay thu được khi quay hình H xung quanh trục Ox.
A. V = π 2 ln 4 3
B. V = 1 2 ln 4 3
C. V = π 2 ln 3 4
D. V = π ln 4 3
Đáp án A
Phương trình hoành độ giao điểm x 4 − x 2 = 0 ⇔ x = 0
Khi đó:
V = π ∫ 0 1 x 4 − x 2 d x = − π 2 ∫ 0 1 d 4 − x 2 4 − x 2 = − π 2 ln 4 − x 2 0 1 = π 2 ln 4 3
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y = x 2 − x 2 , trục tung, đường thẳng x = 1 . Tính thể tích V của khối tròn xoay thu được khi quay hình H quanh trục Ox.
A. V = πln 2 4
B. V = πln 2 2
C. V = ln 2 4
D. V = ln 2 2
cho hình phẳng h được giới hạn bởi đồ thị hàm số y = e mũ 2x trục Ox Oy và đường thẳng x = 2 tính s hình phẳng trên
Tham khảo:
Do \(ex>0;∀xex>0;∀x\)
Diện tích hình phẳng:
\(S=2∫0exdx=ex|20=e2−1\)
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x ln x , trục Ox và đường thẳng x=e
A. S = e 2 + 3 4
B. S = e 2 - 1 2
C. S = e 2 + 1 2
D. S = e 2 + 1 4
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=xlnx, trục Ox và đường thẳng x=e
![]()
![]()
![]()
![]()
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x ln x , trục Ox và đường thẳng x = e
![]()
![]()
![]()
![]()
Đáp án D
Phương pháp:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) , trục Ox, đường thẳng
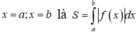
Để tìm đủ cận tích phân ta đi giải phương trình f(x) = 0.
Sử dụng phương pháp tích phân từng phần để tính toán.
Cách giải:

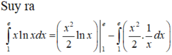
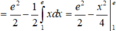
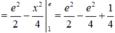
![]()