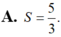
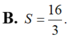
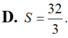
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Tính diện tích hình phằng giới hạn bởi đồ thị các hàm số y = x 2 - x , y = 3 x
A. S = 5 3
B. S = 16 3
C. S = 9
D. S = 32 3
Tính diện tích hình phằng giới hạn bởi đồ thị hàm số y = x 4 - 4 x 2 + 1 và đồ thị hàm số y= x 2 - 3
Phương pháp:
Diện tích hình phẳng giới hạn bởi
đồ thị hàm số y=f(x),y=g(x), các đường thẳng
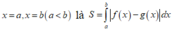
Cách giải:
Xét phương trình hoành độ giao điểm
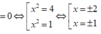
Chọn: A
Tính diện tích hình phằng giới hạn bởi đồ thị hàm số y = x 4 - 4 x 2 + 1 và đồ thị hàm số y = x 2 - 3
A. 8
B. 6
C. 4
D. 2
Cho hàm số y=f(x) liên tục, xác định trên đoạn [a;b]. Diện tích hình phằng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x=a;x=b được tính theo công thức.
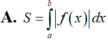
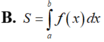
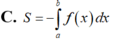
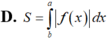
Cho hàm số y = f x liên tục, xác định trên đoạn a ; b . Diện tích hình phằng giới hạn bởi đồ thị hàm số y = f x , trục hoành và hai đường thẳng x = a , x = b được tính theo công thức.
A. S = ∫ a b f x d x
B. S = ∫ a b f x d x
C. S = - ∫ a b f x d x
D. S = - ∫ a b f x d x
Chọn A.
Phương pháp: Theo công thức tính diện tích hình phẳng.
Cách giải: Chọn A.
Cho hình phẳng giới hạn bởi đồ thị các hàm số y = x , đường thẳng y = 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là
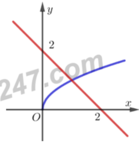
A. 7 6 .
B. 4 3 .
C. 5 6 .
D. 5 4 .
Tính diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số: y = 3 x 2 ; y = 2 x + 5 ; x = - 1 ; x = 2
A. S = 256 27
B. S = 269 27
C. S = 9
D. S = 27
Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = e x ; y = 2 và đường thẳng x =1
A.e-2
B.2ln2-4
C.e+2ln2
D.e+2ln2-4
Chọn D.
Giải PT : e x = 2 ⇔ x = ln 2 Diện tích hình phẳng cần tìm là :
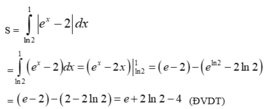
tính diện tích hình giới hạn bởi đồ thị các hàm số y=|x| và y=3
