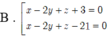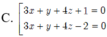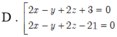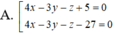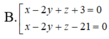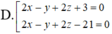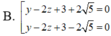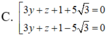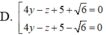Trong không gian với hệ toạ độ Oxyz, cho hai mặt cầu S 1 , S 2 có phương trình lần lượt là x - 2 2 + y - 1 2 + z - 1 2 = 16 và x - 2 2 + y - 1 2 + z - 5 2 = 4 . Gọi (P) là mặt phẳng thay đổi tiếp xúc với cả hai mặt cầu S 1 , S 2 . Khoảng cách lớn nhất từ gốc toạ độ O đến mặt phẳng bằng:
A. 9 2 - 15
B. 15
C. 9 + 15 2
D. 8 3 + 5 2