Xét các số phức z = a + bi thỏa mãn z - 3 - 3 i = 6 Tính P = 3a+b khi biểu thức 2 z + 6 - 3 i + 3 z + 1 + 5 i đạt giá trị nhỏ nhất.
![]()
![]()
![]()
![]()
Xét các số phức z=a+bi z = a + b i ( a , b ∈ R ) thỏa mãn z - 3 + 3 i = 2 . Tính P=a+b khi z - 1 + 3 i + z - 3 + 5 i đạt giá trị lớn nhất
A. 2
B. – 2
C. 8
D. – 8
Xét các số phức z=a+bi (a,b thuộc R) thỏa mãn |z-3-2i|=2. Tính a+b khi |z+1-2i|+2|z-2-5i| đạt giá trị nhỏ nhất
A. 4 - 3
B. 2 + 3
C. 3
D. 4 + 3
Xét các số phức z=a+bi ( a , b ∈ R ) thỏa mãn z - 3 - 2 i = 2 . Tính a+b khi z + 1 - 2 i + 2 z - 2 - 5 i đạt giá trị nhỏ nhất.
![]()
![]()
![]()
![]()
Xét các số phức z = a + b i thỏa mãn z - 3 - 2 i = 2 . Tính a-b biết biểu thức S = z + 1 - 2 i + 2 z - 2 - 5 i đạt giá trị nhỏ nhất.
A. - 3
B. 3
C. 4
D. 0
Chọn A.
Phương pháp: Sử dụng hình học.
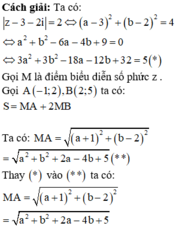

Xét các số phức z = a +bi thỏa mãn z - 3 - 2 i = 2 Tính a-b biết biểu thức S = z + 1 - 2 i + 2 z - 2 - 5 i đạt giá trị nhỏ nhất.
A. - 3
B. 3
C. 4
D. 0
Xét các số phức z = a + bi, (a,b i) thỏa mãn |z – 3 – 3i| = 6. Tính P = 3a + b khi biểu thức 2|z + 6 – 3i| + |z + 1 + 5i| đạt giá trị nhỏ nhất.
A. P = 20
B. P = 2 + 20
C. P = - 20
D. P = - 2 - 20
Đáp án A
Phương pháp:
Cách giải:
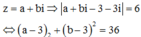
Khi đó ta có:
![]()
![]()
![]()
![]()
Xét các số phức z = a + bi thỏa mãn z - 4 - 3 i = 5 . Tính P = a + b khi z + 1 - 3 i + z - 1 + i đạt giá trị lớn nhất
A. P = 10
B. P = 4
C. P = 6
D. P = 8
Bằng cách ước lượng ta có AN' max khi d là tiếp tuyến của đường tròn và ở xa AB nhất. Dễ tìm được khi đó M ( 6;4 ) nên P = 10
Đáp án cần chọn là A
Cho hai số phức \(z_1,z_2\) thỏa mãn \(\left|z_1+3+2i\right|=1\) và \(\left|z_2+2-i\right|=1\). Xét các số phức \(z=a+bi\), (\(a,b\in R\)) thỏa mãn \(2a-b=0\). Khi biểu thức \(T=\left|z-z_1\right|+\left|z-2z_2\right|\) đạt giá trị nhỏ nhất thì giá trị biểu thức \(P=a^2+b^2\) bằng?
Xét các số phức z = a + b i (a,bÎR) thỏa mãn z - 4 - 3 i = 5 . Tính a+b khi z + 1 - 3 i + z - 1 + i đạt giá trị lớn nhất
A. 10
B. 4
C. 6
D. 8
Xét các số phức z = a + b i , ( a , b ∈ R ) thỏa mãn 4 ( z - z ¯ ) - 15 i = i ( z + z ¯ - 1 ) 2 . Tính F = - a + 4 b khi z - 1 2 + 3 i đạt giá trị nhỏ nhất
![]()
![]()
![]()
![]()