Cho hình thang ABCD vuông tại A và B với A B = B C = A D 2 = a . Quay hình thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của khối tròn xoay được tạo thành
![]()
![]()
![]()
![]()
Cho hình thang vuông ABCD có A ^ = D ^ = 90 0 , AB = AD = 2 cm, DC = 4 cm và BH vuông góc với CD tại H.
a) Chứng minh ∆ABD = ∆HDB.
b) Chứng minh tam giác BHC vuông cân tại H.
c) Tính diện tích hình thang ABCD
Trong không gian với hệ trục tọa độ Oxyz cho hình thang ABCD vuông tại A và B. Ba đỉnh A(1;2;1), B(2;0;1), C(6;1;0) và đỉnh D(a,b,c). Biết rằng hình thang có diện tích là 6 2 , tính a+b+c
A. a+b+c=6
B. a+b+c=8
C. a+b+c=12
D. a+b+c=7
Trong không gian với hệ trục tọa độ Oxyz cho hình thang ABCD vuông tại A và B. Ba đỉnh A(1;2;1), B(2;0;-1), C(6;1;0). Hình thang có diện tích bằng 6√2. Giả sử đỉnh D(a;b;c), tìm mệnh đề đúng?
A. a+b+c=6
B. a+b+c=5
C. a+b+c=8
D. a+b+c=7
Chọn A
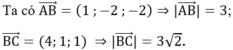
Theo giả thiết ABCD vuông tại A và B và có diện tích bằng 6√2 nên:
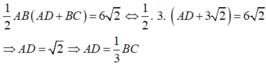
Do ABCD là hình thang vuông tại A và B nên ![]() . Giả sử khi đó ta có:
. Giả sử khi đó ta có:

1.cho hình thang ABCD có ab // cd.tính các góc của hình thang biết
a,d^=54 độ,c^=105độ
b,d^-A^=32độ,b^=2.c^
2.cho tam giác abc vuông tại a.vẽ phía ngoài của tam giác abc một tam giác bcd vuông cân tại b. tứ giác abcd là hình j ? vì sao?
3.cho hình thang abcd (ab// cd)có tia phân giác của góc a và d gặp nhau tại điểm I thuộc cạnh bc. c/m rừng ad bằng tổ của hai đáy
Bài 1:
a.
AB // CD
=> A + D = 1800 (2 góc trong cùng phía)
=> A = 1800 - D = 1800 - 540 = 1260
AB // CD
=> B + C = 1800 (2 góc trong cùng phía)
=> B = 1800 - C = 1800 - 1050 = 750
b.
AB // CD
=> A + D = 1800 (2 góc trong cùng phía)
=> A = (1800 - 320) : 2 = 740
=> D = 1800 - 740 = 1060
AB // CD
=> B + C = 1800 (2 góc trong cùng phía)
=> B = 1800 : (1 + 2) . 2 = 1200
=> C = 1800 - 1200 = 600
Chúc bạn học tốt ^^
mk vừa giả xong bài đó còn hai bài khai thì chưa biết bạn giải giúp mk đc ko ko đc cx chả sao dù j cx cảm ơn bạn
Cho hình thang ABCD vuông tại A và D. Cho biết AB = 15cm, AD = 20cm, các đường chéo AC và BD vuông góc với nhau ở O. Tính :
a, Độ dài các đoạn thẳng OB và OD
b, Độ dài đoạn thẳng AC
c, Diện tích hình thang ABCD
a, Áp dụng các hệ thức lượng trong tam giác vuông ABD, tính được BD = 25cm, OB = 9cm, OD = 16cm
b, Áp dụng các hệ thức lượng trong tam giác vuông DAC tính được OA = 12cm, AC = 100 3 cm
c, Tính được S = 1250 3 c m 2
Cho hình chóp S.ABCD, đáy ABCD là hình thang vuông tại A và D. SA=a căn (3), AB=2a, AD=DC=a. Gọi I là trung điểm AB. SA vuông góc với (ABCD) a. Tính góc giữa mp (SDC) và mp (ABCD) b. Tính góc giữa mp (SDI) và mp (ABCD) c. CM (SCI) vuông góc với (SAB) d. CM (SBC) vuông góc với (SAC)
c.
Từ câu b ta có AICD là hình vuông \(\Rightarrow CI\perp AB\)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp CI\)
\(\Rightarrow CI\perp\left(SAB\right)\)
Lại có \(CI\in\left(SCI\right)\Rightarrow\left(SCI\right)\perp\left(SAB\right)\)
d.
I là trung điểm AB \(\Rightarrow CI\) là trung tuyến ứng với AB
Lại có \(CI=AD=a\) (AICD là hình vuông) \(\Rightarrow CI=\dfrac{1}{2}AB\)
\(\Rightarrow\Delta ACB\) vuông tại C
\(\Rightarrow BC\perp AC\) (1)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(SAC\right)\)
\(BC\in\left(SBC\right)\Rightarrow\left(SBC\right)\perp\left(SAC\right)\)
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{3}\Rightarrow\widehat{SDA}=60^0\)
b.
Gọi E là giao điểm AC và DI
I là trung điểm AB \(\Rightarrow AI=\dfrac{1}{2}AB=a\Rightarrow AI=DC\)
\(\Rightarrow AICD\) là hình bình hành
Mà \(\widehat{A}=90^0\Rightarrow AICD\) là hình chữ nhật
\(AI=AD=a\) (hai cạnh kề bằng nhau) \(\Rightarrow AICD\) là hình vuông
\(\Rightarrow AC\perp DI\) tại E
Lại có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp DI\Rightarrow DI\perp\left(SAE\right)\)
Mà \(DI=\left(SDI\right)\cap\left(ABCD\right)\Rightarrow\widehat{SEA}\) là góc giữa (SDI) và (ABCD)
\(AE=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{AD^2+CD^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow tan\widehat{SEA}=\dfrac{SA}{AE}=\dfrac{\sqrt{6}}{2}\Rightarrow\widehat{SEA}\approx50^046'\)
Cho hình thang ABCD( vuông tại A và D), độ dài cạnh AB bằng 1/3 cạnh DC; độ dài cạnh AD là 4 cm, cạnh AB là 4,5 cm
a, tính diện tích hình thang ABCD
b, nối A với C, B với D cắt nhau ở I. Tính diện tích tam giác BIC
AB=4,5 mà AB=1/3 DC=>DC=4,5*3=13,5
AB+DC=4,5+13,5=18cm
diện tích :18x4 /2=36cm
b)éo biết làm toán lop8 đó banoi
Cho hình thang ABCD vuông tại A và D.Biết CD=2AB=2AD và BC=\(a\sqrt{2}\).
a. TÍnh diện tích hình thang ABCD theo a.
b. Gọi I là trung điểm cùa BC, H là chân đường vuông góc kẻ từ D xuống AC. Chứng minh HDI=45 độ.
Giúp với ạ
a) GỌi E là trung điểm của CD, chi ra ABED là hình vuônng và BEC là tam giác vuông cân.
Từ đó suy ra AB = AD = a, BC = 2a
Diện tích của hình thang ABCD là:
b) = (1) ( 2 góc nhọn có cặp cạnh tương ứng vuông góc)
Xét hai tam giác ADC và IBD vuông tại D và B có:
Suy ra = (2)
Từ (1), (2) =
Mà + = = = hay
cho hình thang vuong abcd. có 2 góc a và d vuông. từ b vẽ BH vuông góc CD nối A với C cắt BH tại G. hãy so sánh diện tích 2 tam giác DGH và GBC
Cho hình thang ABCD vuông tại A và D. Biết AB = 30cm; AD = 25cm; DC = 50cm.
a) Tính: Diện tích hình thang ABCD
b) Tính Diện tích hình tam giác ABC
Giúp tớ với, Please
Diện tích hình thang : ( 30 + 50) x 25 : 2 = 1 000 (cm2)
Diện tích tam giác ADC là : 50 x 25 : 2 = 625 (cm2)
Diện tích 'tam giác ABC là : 1 000 - 625 = 375 (cm2)
đs...