Với x>0, y>0 và x ≠ y và F = ( x + y ) 2 1 ( x - y ) 2 + 1 x y . Tìm Min F.
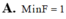
![]()
![]()
Xét biểu thức F(x, y) = 2x + 3y với (x; y) thuộc miền tam giác OAB ở HĐ2. Toạ độ ba đình là O(0, 0), A(150, 0) và B(0; 150) (H.2.5).
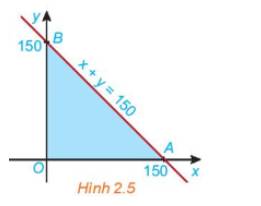
a) Tính giá trị của biểu thức F(x; y) tại mỗi đỉnh O, A và B.
b) Nêu nhận xét về dấu của hoành độ x và tung độ y của điểm (x; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị nhỏ nhất của F(x; y) trên miền tam giác OAB.
c) Nêu nhận xét về tổng x + y của điểm (X; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị lớn nhất của F(x, y) trên miền tam giác OAB.
a) Thay tọa độ điểm O, A, B vào F(x;y) ta được:
F(0;0)=2.0+3.0=0
F(150;0)=2.150+3.0=300
F(0;150)=2.0+3.150=450.
b) Lấy một điểm bất kì trong miền tam giác OAB.
Vì miền OAB là miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\) nên mọi điểm (x;y) thuộc miền OAB thỏa mãn \(x \ge 0\).
Vì miền OAB là miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\) nên mọi điểm (x;y) thuộc miền OAB thỏa mãn \(y \ge 0\).
Vậy \(x \ge 0\) và \(y \ge 0\).
=> \(F\left( {x;y} \right) = 2x + 3y \ge 2.0 + 3.0 = 0\)
Vậy giá trị nhỏ nhất của F(x;y) trên miền OAB là 0.
c) Vì miền OAB là miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\) nên mọi điểm (x;y) thuộc miền OAB thỏa mãn \(x + y \le 150\)
Như vậy với mỗi điểm trong miền tam giác OAB thì đều có tổng \(x + y \le 150\)
Quan sát miền OAB ta thấy điểm B(0;150) là điểm có tung độ lớn nhất nên mọi điểm (x;y) thuộc miền OAB đều có \(y \le 150\).
Vậy ta có: \(F\left( {x;y} \right) = 2x + 3y\)\( = 2.\left( {x + y} \right) + y\)\( \le 2.150 + 150 = 450\)
Dấu “=” xảy ra khi x+y=150 và y=150. Hay x=0, y=150.
Giá trị lớn nhất trên miền OAB là 450 tại điểm B.
Cho hàm số y = f(x) liên tục trên R và a > 0. Giả sử rằng với mọi x ∈ 0 ; a , ta có f(x) > 0 và f(x)f(a – x) = 1. Tính I = ∫ 0 a d x 1 + f ( x ) .
A. a 2 .
B. 2a.
C. a 3 .
D. aln(a + 1).
Chọn A.
Từ giả thiết, suy ra f a - x = 1 f x
Đặt t=a-x suy ra dt=-dx . Đổi cận: x = 0 → t = a x = a → t = 0
Khi đó
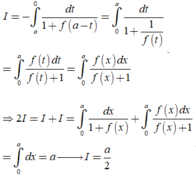
Cho hàm số f(x) liên tục trên R thoả mãn f(0)=0 và | f ( x ) - f ( y ) | ≤ | sin x - sin y | với mọi x , y ∈ R . Giá trị lớn nhất của tích phân ∫ 0 π 2 ( ( f ( x ) ) 2 - f ( x ) ) d x bằng
A. π 4 +1
B. π 8
C. 3 π 8
D. 1- π 4
Giả sử hai hàm số y = f(x) và y = f(x + 0,5) đều liên tục trên đoạn [0; 1] và f(0) = f(1). Chứng minh rằng phương trình f(x) − f(x + 0,5) = 0 luôn có nghiệm trong đoạn [0; 0,5]
Xét hàm số g(x) = f(x) − f(x + 0,5)
Ta có
g(0) = f(0) − f(0 + 0,5) = f(0) − f(0,5)
g(0,5) = f(0,5) − f(0,5 + 0,5) = f(0,5) − f(1) = f(0,5) − f(0)
(vì theo giả thiết f(0) = f(1)).
Do đó,
g ( 0 ) . g ( 0 , 5 ) = [ f ( 0 ) − f ( 0 , 5 ) ] . [ f ( 0 , 5 ) − f ( 0 ) ] = − f ( 0 ) − f ( 0 , 5 ) 2 ≤ 0 .
- Nếu g(0).g(0,5) = 0 thì x = 0 hay x=0,5 là nghiệm của phương trình g(x) = 0
- Nếu g(0).g(0,5) < 0 (1)
Vì y = f(x) và y = f(x + 0,5) đều liên tục trên đoạn [0; 1] nên hàm số y = g(x) cũng liên tục trên [0; 1] và do đó nó liên tục trên [0; 0,5] (2)
Từ (1) và (2) suy ra phương trình g(x) = 0 có ít nhất một nghiệm trong khoảng
Kết luận : Phương trình g(x) = 0 hay f(x) − f(x + 0,5) = 0 luôn có nghiệm trong đoạn (0;0,5)
Cho hàm số y = f(x) xác định và liên tục trên R \ 0 biết x . f x ≠ - 1 ∀ x ≠ 0 f(1) = -2 và với ∀ x ∈ R \ 0 Tính ∫ 1 e f x d x
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho đoạn chương trình:
readln(x,y);
IF x > y THEN F:= 2*x – y ELSE
IF x < y THEN F:= sqr(x) + sqr(y) ELSE F:= 2*x;
Nếu nhập vào từ bàn phím x=0 và y=0 thì giá trị của F là:
A. 13
B. 6
C. 4
D. 0
Tính giá trị biểu thức:
a) F= (1+x/z)*(1-y/z)*(1-z/y) tại x,y,z khác 0 và x+y-z=0
b) G= (x+y)*(y+1)*(x+1) biết x*y=2 và x+y+1=0
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?
a) {y = x + sinx, y = x với 0 ≤ x ≤ π} và {y = x + sinx, y = x với π ≤ x ≤ 2π}
b) {y = sinx, y = 0 với 0 ≤ x ≤ π} và {y = cosx, y = 0 với 0 ≤ x ≤ π};
c) {y = √x, y = x 2 }
và { 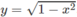 , y = 1 − x}
, y = 1 − x}
Cho hàm số y = f(x) liên tục trên R và thỏa mãn f(-1) > 0 > f(0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f(x), y = 0 và x = 1. Mệnh đề nào sau đây là đúng?
A. S = ∫ - 1 0 f ( x ) d x + ∫ 0 1 f ( x ) d x
B. S = ∫ - 1 1 f ( x ) d x
C. S = ∫ - 1 1 f ( x ) d x
D. S = ∫ - 1 1 f ( x ) d x