Trong mặt phẳng phức, gọi M là điểm biểu diễn cho số phức z - z 2 với z = a + bi Chọn kết luận đúng
A. M thuộc tia Ox.
B. M thuộc tia Oy
C. M thuộc tia đối của tia Ox.
D. M thuộc tia đối của tia Oy.
Trong mặt phẳng phức gọi M là điểm biểu diễn cho số phức z = a + bi (a, b Î R, ab ¹ 0 ), M' là điểm biểu diễn cho số phức z → . Mệnh đề nào sau đây đúng?
A. M' đối xứng với M qua Oy
B. M' đối xứng với M qua Ox
C. M' đối xứng với M qua đường thẳng y = x.
D. M' đối xứng với M qua O
Đáp án B
Ta có M’ là điểm biễu diễn cho số phức z → = a - b i Þ M’(a; -b) nên M’ đối xứng với M qua Ox
Trong mặt phẳng tọa độ Oxy , gọi M là điểm biểu diễn số phức z = 12 - 5 i , M’ là điểm biểu diễn cho số phức z ' = 1 + i 2 z . Tính diện tích tam giác OMM’.
A. 169 5 2
B. 169 4
C. 169 2 4
D. 169 2
Chọn B.
Phương pháp: Tìm tọa độ các điểm sau đó tính diện tích tam giác. Lưu ý trong tam giác ABC

Trong mặt phẳng phức, gọi M là điểm biểu diễn cho số phức ( z - z ¯ ) 2 với z = a + b i ( a , b ∈ ℝ , b ≠ 0 )
Chọn kết luận đúng
A. M thuộc tia Ox.
B. M thuộc tia Oy
C. M thuộc tia đối của tia Ox.
D. M thuộc tia đối của tia Oy.
Đáp án C
Phương pháp.
Tính trực tiếp ![]()
Lời giải chi tiết.
Ta có

Do ![]()
Do đó M có phần thực âm, phần ảo bằng 0, nên thuộc tia đối của tia Ox.
Trong mặt phẳng phức, gọi M là điểm biểu diễn cho số phức ( z - z ¯ ) 2 với z= a+bi(a, b ∈ R , b ≠ 0 ). Chọn kết luận đúng
A. M thuộc tia Ox
B. M thuộc tia Oy
C. M thuộc tia đối của tia Ox
D. M thuộc tia đối của tia Oy
Trong mặt phẳng phức, gọi M là điểm biểu diễn cho số phức ( z - z ¯ ) 2 v ớ i z = a + b i ( a , b ∈ ℝ , b ≠ 0 ) . Chọng kết luận đúng.
![]()
![]()
![]()
![]()
Trong mặt phẳng phức, gọi M là điểm biểu diễn số phức z - z - 2 với z = a + bi(a,b ϵ R,b≠0)
A. M thuộc tia đối Oy
B. M thuộc tia Oy
C. M thuộc tia đối của tia Ox
D. M thuộc tia Ox
Cho số phức z thỏa mãn |z + 2| + |z – 2| = 8. Trong mặt phẳng phức tập hợp những điểm M biểu diễn cho số phức z là?

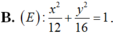
C. ( x + 2) 2 + ( y - 2) 2 = 64.
D. ( x + 2) 2 + ( y - 2) 2 = 8.
Chọn A.
Gọi M(x; y) , F1= ( -2; 0) và F2( 2; 0).
Ta có |z + 2| + |z – 2| = 8 ![]()
Hay MF1+ MF2 = 8.
Do đó điểm M(x; y) nằm trên elip (E ) có 2a = 8 nên a = 4
ta có F1F2 = 2c nên 4 = 2c hay c = 2
Ta có b2 = a2 - c2 = 16 - 4 = 12
Vậy tập hợp các điểm M là elip 
Trong mặt phẳng phức, gọi M là điểm biểu diễn số phức ( z - z ¯ ) 2 với z = a+bi(a,b ∈ ℝ , b ≠ 0). Chọn kết luận đúng.
A. M thuộc tia Ox
B. M thuộc tia Oy
C. M thuộc tia đối của tia Ox
D. M thuộc tia đối của tia Oy
Đáp án C
Gọi ![]()
![]()
Suy ra M thuộc tia đối của tia Ox.
Trong mặt phẳng phức, gọi M là điểm biểu diễn số phức z − z ¯ 2 với z = a + b i a , b ∈ ℝ , b ≠ 0 . Chọn kết luận đúng
A. M thuộc tia Ox
B. M thuộc tia Oy
C. M thuộc tia đối của tia Ox
D. M thuộc tia đối của tia
Đáp án C
Gọi w = z − z ¯ 2 = a + b i − a + b i 2 = 0 = − 4 b 2
Suy ra M thuộc tia đối của tia Ox