Tìm giá trị nhỏ nhất (min y) của y = x x khi x ∈ 0 ; + ∞
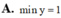
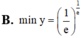
![]()
![]()
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Tìm giá trị nhỏ nhất của hàm số y = 1 x 3 − 1 x khi x > 0
A. 2 3 9
B. − 1 4
C. 0
D. − 2 3 9
Đáp án A
Xét hàm số f x = y = 1 x 3 − 1 x trên 0 ; + ∞ , có f ' x = x 2 − 3 x 4 , ∀ x < 0
Phương trình:
f ' x < 0 ⇔ x < 0 x 2 − 3 = 0 ⇔ x < 0 x − 3 x + 3 = 0 ⇒ x = − 3
Tính f − 3 = 2 3 9 ;
lim x → 0 f x = + ∞ . lim x → + ∞ f x = − ∞
Vậy min 0 ; + ∞ f x = 2 3 9
Cho hàm số f ( x ) = a x 4 + b x 2 + c có m i n ( - ∞ ; 0 ) f ( x ) = f ( - 1 ) . Giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [ 1 2 ;2] bằng
A. c + 8a
B. c - 7 16 a
C. c + 9 16 a
D. c - a
Cho x, y > 0, x + y ≤ 5. Tìm giá trị nhỏ nhất của A = x + y + 8/x + 18/ y
ta có \(x+y\le5=>-\left(x+y\right)\ge-5\)
có \(A=x+y+\dfrac{8}{x}+\dfrac{18}{y}=-\left(x+y\right)+2x+2y+\dfrac{8}{x}+\dfrac{18}{y}\)
có \(-\left(x+y\right)+2x+2y+\dfrac{8}{x}+\dfrac{18}{y}\ge-5+8+12=15\)
=>A\(\ge15\) dấu= xảy ra <=>x=2,y=3
vậy min A=15
Cho bài toán: “Tìm Giá trị lớn nhất, giá tri nhỏ nhất của hàm số y = f ( x ) = x + 1 x - 1 trên - 2 ; 3 2 ?”. Một học sinh giải như sau:
Bước 1: y ' = 1 - 1 ( x - 1 ) 2 ∀ x ≢ 1
Bước 2: y ' = 0 ⇔ x = 2 ( L ) x = 0
Bước 3: f ( - 2 ) = - 7 3 ; f ( 0 ) = - 1 ; f 3 2 = 7 2 Vậy m a x [ - 2 ; 3 2 ] f ( x ) = 7 3 ; m i n [ - 2 ; 3 2 ] = - 7 3
Lời giải trên đúng hay sai ? Nêu sai thì sai lừ bưóc nào ?
A. Lời giải trên hoàn toàn đúng
B. Lời giải trên sai từ bước 1
C. Lời giải trên sai từ bước 2
D. Lời giải trên sai từ bước 3
Tìm số tự nhiên nhỏ nhất khác 0 mà khi nhân nó với 135 ta được một số chính phương:
Giá trị của x và y để biểu thức A= |x + 15| +|-25-y| - 79 đạt giá trị nhỏ nhất là ?
dễ thì làm đi nguyenmanhtrung
Hãy vẽ đồ thị của các hàm số y = 2x2, y = -2x2. Dựa vào đồ thị để trả lời các câu hỏi sau:
Nếu a > 0 thì hàm số y = ax2 đồng biến khi nào? Nghịch biến khi nào?
Với giá trị nào của x thì hàm số đạt giá trị nhỏ nhất? Có giá trị nào của x để hàm số đạt giá trị lớn nhất không?
Nếu a < 0 thì hàm số đồng biến khi nào? Nghịch biến khi nào? Với giá trị nào của x thì hàm số đạt giá trị lớn nhất? Có giá trị nào của x để hàm số đạt giá trị nhỏ nhất không?
Vẽ hình:
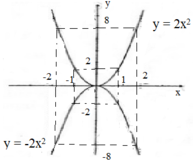
Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
Cho 2 số thực x ; y thỏa mãn 0 < x ≤ 1 , 0 < y ≤ 1 và x + y = 3xy . Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x2 + y2 - 4xy
Cho x > 0; y > 0 và x+y<=4/3 . Tìm giá trị nhỏ nhất của biểu thức M=x+y+1/x+1/y
Áp dụng BĐT cosi cho \(x,y>0\)
\(M=x+y+\dfrac{1}{x}+\dfrac{1}{y}\ge2\sqrt{x\cdot\dfrac{1}{x}}+2\sqrt{y\cdot\dfrac{1}{y}}=4\)
Dấu \("="\Leftrightarrow x=y=1\)
Mà \(x+y=2\le\dfrac{4}{3}\left(vô.lí\right)\) nên dấu \("="\) không xảy ra
Vậy M không có GTNN
Hãy vẽ đồ thị của các hàm số y = 2 x 2 , y = - 2 x 2 . Dựa vào đồ thị để trả lời các câu hỏi sau:
a) Nếu a > 0 thì hàm số y = a x 2 đồng biến khi nào? Nghịch biến khi nào?
Với giá trị nào của x thì hàm số đạt giá trị nhỏ nhất? Có giá trị nào của x để hàm số đạt giá trị lớn nhất không?
Nếu a < 0 thì hàm số đồng biến khi nào? Nghịch biến khi nào? Với giá trị nào của x thì hàm số đạt giá trị lớn nhất? Có giá trị nào của x để hàm số đạt giá trị nhỏ nhất không?
b) Đồ thị của hàm số y = a x 2 có những đặc điểm gì (trường hợp a > 0 , trường hợp a < 0)
Vẽ hình:
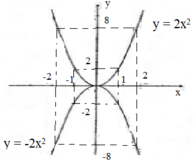
a) Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
b) Đồ thị hàm số y = a x 2 là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.