Tập hợp các số thực m thỏa mãn hàm số y = m x 4 - x 2 + 1 có đúng 1 điểm cực trị là
A. - ∞ ; 0
B. ( - ∞ ; 0 ]
C. 0 ; + ∞
D. [ 0 ; ∞ )
Tập hợp các số thực m thỏa mãn hàm số y = m x 4 - x 2 + 1 có đúng 1 điểm cực trị là
A. (-∞;0)
B. (-∞;0]
C. (0;+∞)
D. [0;+∞)
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 x 2 + a 2 - 2 n - 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 , e 2 y = 1 . Số phần tử của S là:
A. 0
B. 1
C. 2
D. Vô số
Xét hàm số f ( t ) = 9 t 9 t + m 2 với là m tham số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho f(x) + f(y) =1 với mọi số thực x, y thỏa mãn e x + y ≤ e ( x + y ) . Tìm số phần tử của S.
A. 0
B. 1
C. Vô số
D. 2
Tập hợp tất cả các giá trị thực của tham số m để hàm số \(y=\left|x^3-3x^2+m-4\right|\) có đúng 5 điểm cực trị là?
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 ; e 2 y = 1 . Số phần tử của S là:/
A. 0
B. 1
C. 2
D. Vô số
Chọn B
Cách giải: Ta có:
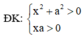
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0
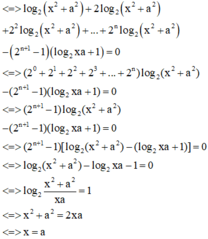
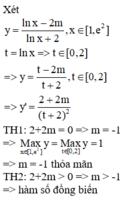
![]()
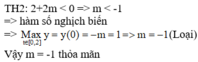
tìm tất cả các giá trị của m sao cho đồ thị hàm số cắt đồ thị hàm số tại \(y=x^2+2mx+4\) đúng 2 điểm phân biệt có hoành độ thỏa mãn
Cho hàm số y = ln ( 2 x - a ) - 2 m ln ( 2 x - a ) + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + . . . + log . . . 2 ( x 2 + a 2 ) - ( 2 n + 1 - 1 ) ( log 2 x a + 1 ) = 0
(với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thoả mãn m a x [ 1 ; e 2 ] y = 1 . Số phần tử của S là
A. 0
B. 1
C. 2
D. Vô số
Cho hàm số y=f(x) có đạo hàm liên tục trên ℝ . Hàm số y=f '(x) có đồ thị như hình vẽ bên dưới. Tìm tập hợp S tất cả các giá trị thực của tham số m để hàm số g x = 2 f 2 x + 3 f x + m có đúng 7 điểm cực trị, biết f a = 1 , f b = 0 , lim x → + ∞ f x = + ∞ , lim x → − ∞ f x = − ∞
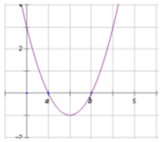
A. S = − 5 ; 0
B. S = − 8 ; 0
C. S = − 8 ; 1 6
D. S = − 5 ; 9 8
A
Từ đồ thị hàm số y=f '(x) ta có bảng biến thiên
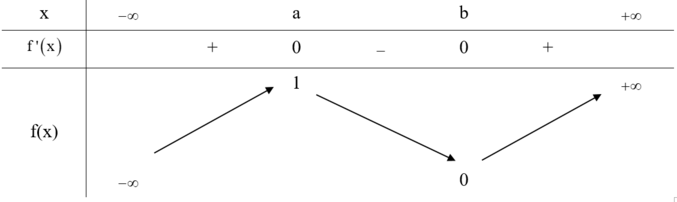
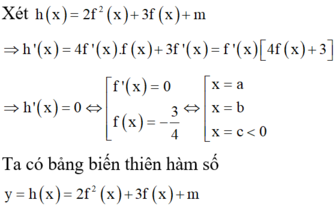

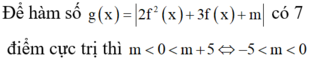
Tìm tất cả các giá trị thực của tham số m để hàm số y = 1 3 x 3 - ( m - 1 ) x 2 + 4 ( m - 2 ) x + 2 có hai cực trị x 1 , x 2 thỏa mãn x 2 1 + x 2 2 + 3 x 1 x 2 = 4
A. m= -2 hoặc m = -1
B. m = -1 hoặc m = 2
C. m = - 1 ± 21
D. Không tồn tại m