Một vật chuyển động với phương trình s t = 4 t 2 + t 3 , trong đó t > 0, t tính bằng s, s(t) tính bằng m. Tìm gia tốc của vật tại thời điểm vận tốc của vật bằng 11 m / s .
A. 13 m / s 2
B. 11 m / s 2
C. 12 m / s 2
D. 14 m / s 2
Một vật chuyển động với phương trình s ( t ) = 4 t 2 + t 3 , trong đó t > 0 , t tính bằng s, s(t) tính bằng m. Tìm gia tốc của vật tại thời điểm vận tốc của vật bằng 11(m/s).
![]()
![]()
![]()
![]()
Một vật chuyển động với phương trình s t = 4 t 2 + t 3 , trong đó t>0,t tính bằng s,s(t) tính bằng m Tìm gia tốc của vật tại thời điểm vận tốc của vật bằng 11
A.13m/s2.
B. 11m/s2.
C. 12m/s2.
D. 14m/s2.
Một vật chuyển động với phương trình s t = 4 t 2 + t 3 , trong đó t > 0 , t tính bằng s, s(t) tính bằng m. Tìm gia tốc của vật tại thời điểm vận tốc của vật bằng 11.
A. 13m/s2.
B. 11m/s2.
C. 12m/s2.
D. 14m/s2.
Đáp án D
Ta có:
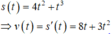
Vận tốc đạt 11 tại thời điểm
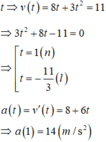
Một vật chuyển động thẳng xác định bởi phương trình S = t 3 - 3 t 2 + 5 t + 1 , trong đó t tính bằng giây (s), S tính bằng mét. Vận tốc chuyển động của vật đó khi t=3 là:
A. 24(m/s)
B. 17(m/s)
C. 14(m/s)
D. 12(m/s)
Một vật chuyển động thẳng xác định bởi phương trình S = t 3 − 3 t 2 + 5 t + 1 trong đó t tính bằng giây và S tính bằng mét. Vận tốc chuyển động của vật đó khi t=3 là
A. 12 (m/s)
B. 14 (m/s)
C. 17 (m/s)
D. 24 (m/s)
Đáp án B
Vận tốc của vật xác định bởi phương trình v = s ' = 3 t 2 − 6 t + 5 ⇒ v 3 = 14 m / s
Vị trí của một vật chuyển động thẳng được cho bởi phương trình: \(s = f(t) = {t^3} - 6{t^2} + 9t\), trong đó t tính bằng giây và s tính bằng mét.
a) Tính vận tốc của vật tại các thời điểm t = 2 giây và t = 4 giây.
b) Tại những thời điểm nào vật đứng yên?
c) Tìm gia tốc của vật tại thời điểm t = 4 giây.
d) Tính tổng quãng đường vật đi được trong 5 giây đầu tiên.
e) Trong 5 giây đầu tiên, khi nào vật tăng tốc, khi nào vật giảm tốc?
\(a,v\left(t\right)=s'\left(t\right)=3t^2-12t-9\)
Vận tốc của vật tại thời điểm t = 2s là: \(v\left(2\right)=3\cdot2^2-12\cdot2+9=-3\left(m/s\right)\)
Vận tốc của vật tại thời điểm t = 4s là: \(v\left(4\right)=3\cdot4^2-12\cdot4+9=9\left(m/s\right)\)
b, Khi vật đứng yên, ta có:
\(v\left(t\right)=0\Leftrightarrow3t^2-12t+9=0\Leftrightarrow\left[{}\begin{matrix}t=3\\t=1\end{matrix}\right.\)
c, Ta có \(a\left(t\right)=s"\left(t\right)=6t-12\)
Gia tốc của vật tại thời điểm t = 4s là \(a\left(4\right)=6\cdot4-12=12\left(m/s^2\right)\)
d, Ta có: Khi t = 1s hoặc t = 3s thì vật đứng yên.
Như vậy, ta cần tính riêng quãng đường vật đi được từng khoảng thời gian \(\left[0;1\right],\left[1;3\right],\left[3;5\right]\)
Từ thời điểm t = 0s đến thời điểm t = 1s, vật đi được quãng đường là:
\(\left|f\left(1\right)-f\left(0\right)\right|=\left|4-0\right|=4m\)
Từ thời điểm t = 1s đến thời điểm t = 3s, vật đi được quãng đường là:
\(\left|f\left(3\right)-f\left(1\right)\right|=\left|0-4\right|=4m\)
Từ thời điểm t = 3s đến thời điểm t = 5s, vật đi được quãng đường là:
\(\left|f\left(5\right)-f\left(3\right)\right|=\left|20-0\right|=20m\)
Tổng quãng đường vật đi được trong 5s đầu tiên là: 28m
e,Xét \(a\left(t\right)=0\Leftrightarrow t=2\)
Với \(t\in[0;2)\) thì gia tốc âm, tức là vật giảm tốc.
Với \(t\in(2;5]\) thì gia tốc dương, tức là vật tăng tốc.
Phương trình vận tốc của một vật chuyển động thẳng là vt = 5 + 2t với vt tính bằng m/s, t tính bằng s. 1. Chuyển động của vật thuộc loại gì? 2. Tìm phương trình đường đi trong chuyển động đó. 3. Tính đường đi của vật từ thời điểm t1=4s đến thời điểm t2=6s.
Một chất điểm chuyển động trong 20 giây đầu tiên có phương trình s ( t ) = 1 12 t 4 - t 3 + 6 t 2 + 10 t , trong đó t > 0 với t tính bằng giây (s) và s(t) tính bằng mét (m). Hỏi tại thời điếm gia tốc của vật đạt giá trị nhỏ nhất thì vận tốc của vật bằng bao nhiêu:
![]()
![]()
![]()
Một chuyển động thẳng xác định bởi phương trình \(s\left( t \right) = 4{t^3} + 6t + 2\), trong đó \(s\) tính bằng mét và \(t\) là thời gian tính bằng giây. Tính vận tốc tức thời của chuyển động tại \(t = 2\).
Vận tốc tức thời của chuyển động tại \(t = 2\) là:
\(\begin{array}{l}v\left( 2 \right) = s'\left( 2 \right) = \mathop {\lim }\limits_{t \to 2} \frac{{s\left( t \right) - s\left( 2 \right)}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{\left( {4{t^3} + 6t + 2} \right) - \left( {{{4.2}^3} + 6.2 + 2} \right)}}{{t - 2}}\\ = \mathop {\lim }\limits_{t \to 2} \frac{{4{t^3} + 6t + 2 - 46}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{4{t^3} + 6t - 44}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{2\left( {t - 2} \right)\left( {2{t^2} + 4t + 11} \right)}}{{t - 2}}\\ = \mathop {\lim }\limits_{t \to 2} 2\left( {2{t^2} + 4t + 11} \right) = 2\left( {{{2.2}^2} + 4.2 + 11} \right) = 54\end{array}\)
Vậy vận tốc tức thời của chuyển động lúc \(t = 2\) là: \(v\left( 2 \right) = 54\left( {m/s} \right)\)