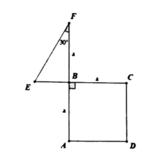
Cho mô hình (như hình vẽ) với tam giác EFB vuông tại B, cạnh FB= a, E F B ^ = 30 ° và tứ giác ABCD là hình vuông. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh cạnh AF
A. V = 4 / 3 a 3
B. V= 10/9 a 3
C. V= 4/3 π a 3
D. V= 10/9 π a 3