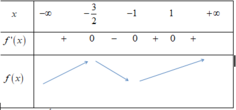
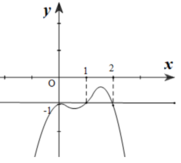
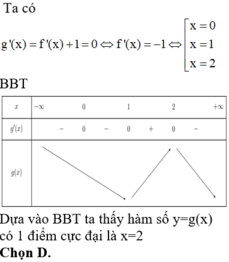
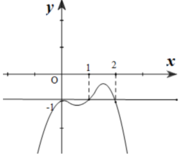
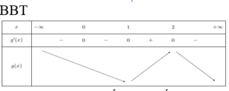
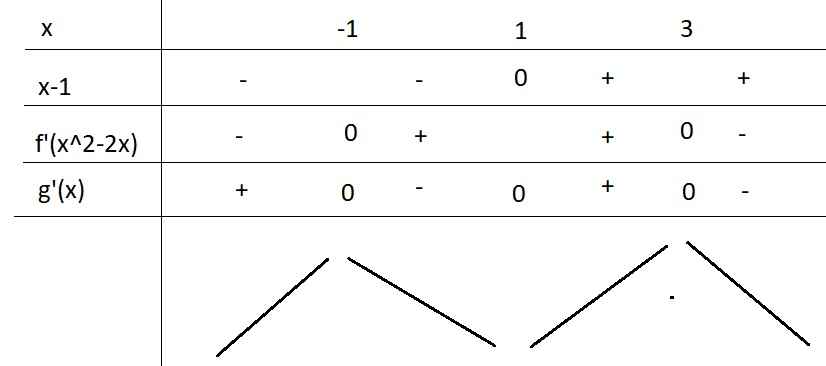
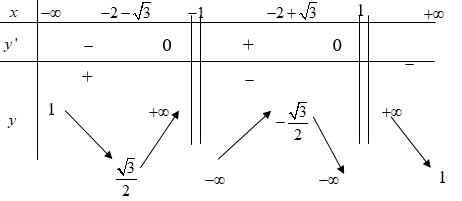
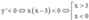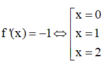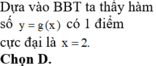Cho hàm số y=f(x) xác định trên R ∖ { - 1 ; 1 } liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau.
Tìm tập hợp tất cả các giá trị của tham số m sao cho phương trình f(x)=m có đúng 1 nghiệm.
A. { - 3 2 ; 3 2 ; 1 }
B. { - 3 2 ; 3 2 }
C. { 1 }
D. ( 1 ; + ∞ )