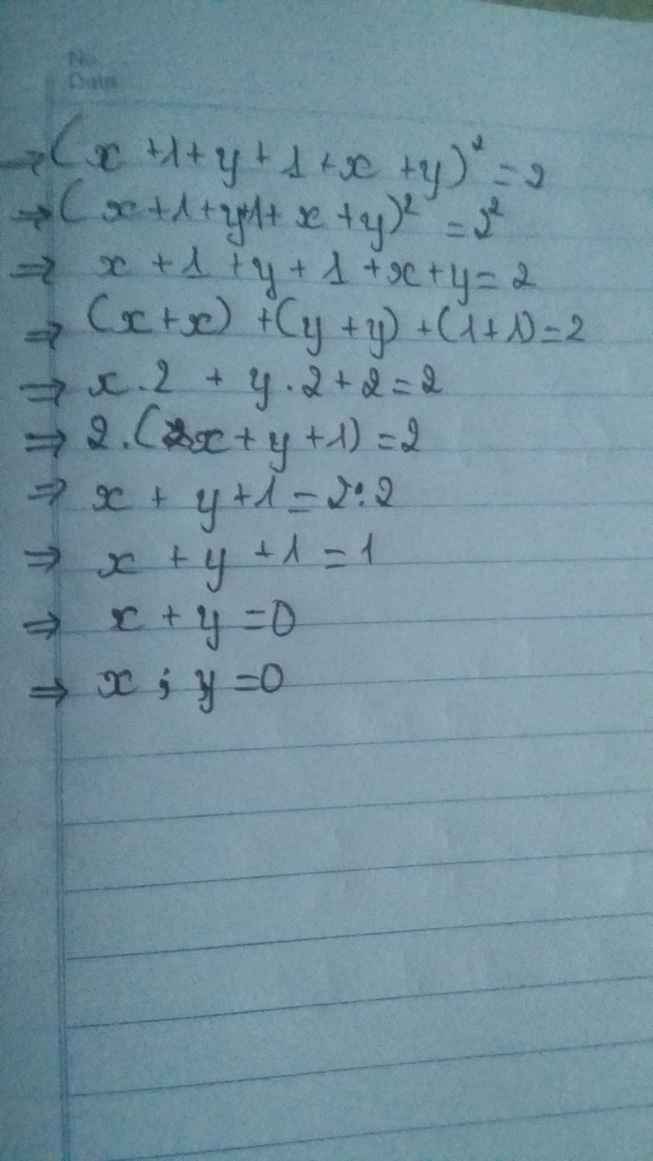Tìm x,y nguyên sao cho (x+y)2 = (x-1)(y+1)
NT
Những câu hỏi liên quan
Tìm các số nguyên x, y sao cho (x-3).(y+2)=5
Tìm các số nguyên x, y sao cho (x-2).(y+1)=5
Ai đó giúp mk với ![]()
a) Ta có: (x-3)(y+2)=5
nên (x-3) và (y+2) là ước của 5
\(\Leftrightarrow x-3;y+2\in\left\{1;-5;-1;5\right\}\)
Trường hợp 1:
\(\left\{{}\begin{matrix}x-3=1\\y+2=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=3\end{matrix}\right.\)
Trường hợp 2:
\(\left\{{}\begin{matrix}x-3=5\\y+2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=8\\y=-1\end{matrix}\right.\)
Trường hợp 3:
\(\left\{{}\begin{matrix}x-3=-1\\y+2=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-7\end{matrix}\right.\)
Trường hợp 4:
\(\left\{{}\begin{matrix}x-3=-5\\y+2=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-3\end{matrix}\right.\)
Vậy: \(\left(x,y\right)\in\left\{\left(4;3\right);\left(8;-1\right);\left(2;-7\right);\left(-2;-3\right)\right\}\)
b) Ta có: (x-2)(y+1)=5
nên x-2 và y+1 là các ước của 5
\(\Leftrightarrow x-2;y+1\in\left\{1;-1;5;-5\right\}\)
Trường hợp 1:
\(\left\{{}\begin{matrix}x-2=1\\y+1=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=4\end{matrix}\right.\)
Trường hợp 2:
\(\left\{{}\begin{matrix}x-2=5\\y+1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=7\\y=0\end{matrix}\right.\)
Trường hợp 3:
\(\left\{{}\begin{matrix}x-2=-1\\y+1=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-6\end{matrix}\right.\)
Trường hợp 4:
\(\left\{{}\begin{matrix}x-2=-5\\y+1=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-2\end{matrix}\right.\)
Vậy: \(\left(x,y\right)\in\left\{\left(3;4\right);\left(7;0\right);\left(1;-6\right);\left(-3;-2\right)\right\}\)
Đúng 3
Bình luận (0)
Tìm số nguyên x ,y sao cho (x+1)2+(y+1)2+(x-y)2=2
1)Tìm tất cả các số nguyên dương n sao cho :2n-1 chia hết cho 7
2)Tìm số nguyên x,y sao cho :|x-1|+|x-2|+|y-3|+|y-4|=3
Tìm số nguyên x, y sao cho (x+1)^2+(y+1)^2+(x-y)^2=2
\(\left(x+1\right)^2+\left(y+1\right)^2+\left(x-y\right)^2=2\Rightarrow\left(x+1\right)^2\le2\Rightarrow\orbr{\begin{cases}\left(x+1\right)^2=0\\\left(x+1\right)^2=1\end{cases}}\)
- \(\left(x+1\right)^2=0\Leftrightarrow x=-1\).
Với \(x=-1\): \(\left(y+1\right)^2+\left(y+1\right)^2=2\Leftrightarrow\orbr{\begin{cases}y=-2\\y=0\end{cases}}\).
- \(\left(x+1\right)^2=1\Leftrightarrow\orbr{\begin{cases}x=0\\x=-2\end{cases}}\).
Với \(x=0\): \(1+\left(y+1\right)^2+y^2=2\Leftrightarrow2y^2+2y=0\Leftrightarrow\orbr{\begin{cases}y=0\\y=-1\end{cases}}\).
Với \(x=-2\): \(1+\left(y+1\right)^2+\left(y+2\right)^2=2\Leftrightarrow2y^2+6y+4=0\Leftrightarrow\orbr{\begin{cases}y=-1\\y=-2\end{cases}}\).
Vậy \(\left(x,y\right)\in\left\{\left(0,0\right),\left(0,-1\right),\left(-2,-1\right),\left(-2,-2\right),\left(-1,-2\right),\left(-1,0\right)\right\}\).
Tìm x,y thuộc n sao để x^3y-x^2y+4x^2+5xy-y^2=0
tìm số nguyên x,y sao cho x(x^2-y)+y+3)(x^2+1)=0
1.a) Tìm các cặp số nguyên (x;y) sao cho: (x-1)/5 = 3/(y+4)
b) Tìm các số nguyên x sao cho số P=(x-2)/(x+1)
tìm số nguyên x,y sao cho:
(x+1)x(y-2)=2
(x+1)x(y-2) =2
\(\left[{}\begin{matrix}x=0;y=4\\x=-2;y=0\\x=1;y=3\\x=-3;y=1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Bài 1: Tìm x, y nguyên dương thỏa mãn đẳng thức: 1!+2!+3!+...+x!=y2
Bài 2: Tìm (x; y) nguyên sao cho: \(2013^{||x^2-y|-8|+y^2-1}=1\)
Bài 2 :
=> ||x^2-y|-8|+y^2+1 = 0
Mà ||x^2-y|-8| >= 0 ; y^2 >= 0
=> ||x^2-y|-8| + y^2 + 1 > 0
=> ko tồn tại x,y tm bài toán
Tk mk nha
Đúng 0
Bình luận (0)
Tìm x , y là số nguyên sao cho :
( x +1 )^2 + ( y +1 )^2 +( x - y)^2 = 2
ta thấy 2 >0
nên (x+1)^2 + (y+1)^2 +(x-y)^2 = x+1 + y+1 + x -y = 2
=> 2x =2
=> x = 1
tự tìm y nhé bn
Đúng 0
Bình luận (0)