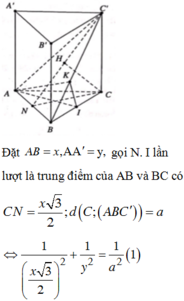
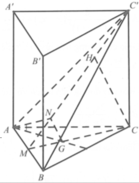
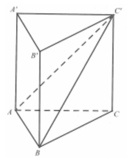
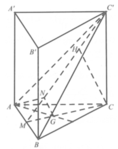
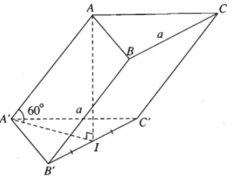
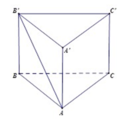
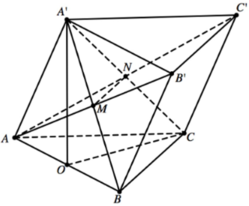
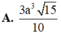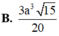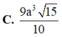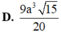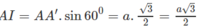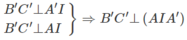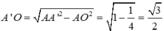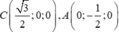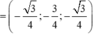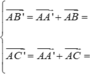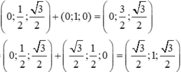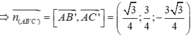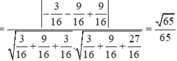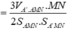Cho hình lăng trụ đều A B C . A ' B ' C ' biết góc giữa hai mặt phẳng A ' B C và A B C bằng 45 ° , diện tích tam giác A ' B C bằng a 2 6 . Tính diện tích xung quanh của hình trụ ngoại tiếp hình lăng trụ A B C . A ' B ' C ' .
A. 4 π a 2 3 3
B. 2 π a 2
C. 4 π a 2
D. 8 π a 2 3 3