△ ABC vuông tại A. M là trung điểm cạnh huyền BC. Hạ M H ⊥ A B , M K ⊥ A C Cho △ ABC và hình chữ nhật AHMK quay quanh AB tạo thành các khối tròn xoay có thể tích V1, V2. Tính k = V 2 V 1
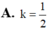
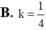
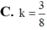
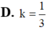
cho tam giác vuông ABC vuông tại A và M là trung điểm của BC, hãy chỉ ra cạnh huyền, cạnh góc vuông, trung tuyến ứng với cạnh huyền. A cho cạnh AB=9cm, AC=12cm. tính BC,MA, diện tích tam giác ABC,ABM? B cho góc B bằng 45 độ, tính góc C, chứng minh tam giác ABC vuông cân và AM vuông góc với bc. tính AM
Cho tam giác ABC vuông tại B, hạ đường cao BH tới cạnh huyền. Gọi M là trung điểm
của HC và K là trực tâm tam giác ABM. Từ A kẻ tia Ax song song với BC và nằm cùng phía
với C trên nửa mặt phẳng bờ là đường thẳng AB. Trên tia Ax điểm P sao cho
AP = 1/2 BC.
Chứng minh rằng:
1. K là trung điểm BH.
2. Tứ giác AKMP là hình bình hành.
3.PM ⊥ BM .
Cho △ABC vuông tại A,lấy điểm M thuộc cạnh huyền BC(M không chung B và C).Gọi D và E thứ tự là chân đường vuông góc kẻ từ M đến AB,AC.
a,Tứ giác AEMD là hình gì?
b,Gọi P là điểm đối xứng của M quaD,K là điểm đối xứng của M qua E và I là trung điểm của DE.Chứng minh P đối xứng với K qua A.
c,Khi M chuyển động trên đoạn BC thì I chuyển động trên đường nào?
a: Xét tứ giác AEMD có
\(\widehat{AEM}=\widehat{ADM}=\widehat{DAE}=90^0\)
Do đó: AEMD là hình chữ nhật
Cho ∆ABC vuông tại A,gọi M là trung điểm của cạnh BC . từ M kẻ MH vuông góc với AB tại H , MK vuông góc với AC tại K. 1) Chứng minh tứ giác AHMK là hình chữ nhật. 2) Gọi E là trung điểm của HM .Chứng minh : a) H là trung điểm của AB. b) Ba điểm B,E,K thẳng hàng. 3) Kẻ Ax song song với BC , cắt tia MK tại D . Chứng minh : a) Tứ giác ABMD là hình bình hành? Từ đó suy ra AD=AM. b) Tứ giác AMCD là hình thoi.
1: Xét tứ giác AHMK có
góc AHM=góc AKM=góc HAK=90 độ
=>AHMK là hình chữ nhật
2:
a: Xét ΔABC có
M là trung điểm của BC
MH//AC
Do đó: H là trung điểm của AB
b: Xét ΔABC có
M là trung điểm của CB
MK//AB
Do đó: K là trung điểm của AC
Xét ΔABC có MK//AB
nên MK/AB=CM/CB=1/2
=>MK=1/2AB=HB
Xét tứ giác BHKM có
BH//KM
BH=KM
Do đó: BHKM là hình bình hành
=>BK cắt HM tại trung điểm của mỗi đường
=>B,E,K thẳng hàng
3:
a: Xét tứ giác ABMD có
AB//DM
AD//BM
Do đó: ABMD là hình bình hành
=>AD=MB=AM
b: Xét tứ giác AMCD có
AM//CD
AM=CD
AD=AM
Do đó: AMCD là hình thoi
Cho tam giác ABC vuông tại A. Vẽ phía ngoài tam giác ABC 2 tam giác vuông cân ADB( cạnh huyền AB) và AEC( cạnh huyền AC). Gọi M là trung điểm của BC, I là giao điểm của DM với AB và K là giao điểm của EM với AC
a, BDEC là hình thang
b,AKMI là hình chữ nhật
c, Tam giác DME là tam giác vuông cân
Cho tam giác ABC vuông cân tại A, M là trung điểm của cạnh BC,E là điểm nằm giữa M và C. Vẽ BH vuông góc với AE tại H, CK vuông góc với AE tại K. CMR BH=A
Cho tam giác ABC vuông tại A lấy điểm M thuộc cạnh huyền Bc (M ko trung B và C).Gọi D và E theo thứ tự là chân đường vuông góc kẻ từ M đến AB,AC
a) Tứ giác AEMD là hình gì ?
b) Gọi P là điểm đối xứng của M qua D,K là điểm đối xứng của M qua E và I là trung điểm của DE.Chứng minh P dối xứng với K qua A
các bn giải nhanh hộ mk với mk đang cần gấp O_O !
Cho tam giác ABC vuông tại A; đường cao AH. Gọi K, D lần lượt là hình chiếu của H trên các cạnh AB, AC; I là trung điểm AH. C/m rằng a, Tứ giác AKHD là hcn b,K đối xứng với D qua I c, Gọi M là trung điểm BC. C/m góc BAH = góc CM d, C/m KD vuông góc AM e, Gọi E, F lần lượt là trung điểm BH và CK. C/m KE song song DF
Cho tam giác ABC cân tại A, BH vuông góc AC tại H. Trên cạnh BC lấy
điểm M bất kì ( khác B và C). Gọi D, E, F là chân đường vuông góc hạ từ M đến AB, AC,
BH.
a) Chứng minh ∆DBM = ∆FMB.
b) Chứng minh khi M chạy trên cạnh BC thì tổng MD + ME có giá trị không đổi.
c) Trên tia đối của tia CA lấy điểm K sao cho CK = EH. Chứng minh BC đi qua
trung điểm của DK.
Giải thích các bước giải:a) FM// HC (\(\perp\)AC)\(\Rightarrow\)góc FMB=góc BCH mà BCH=DBM ( tam giác ABC cân tại A)
Xét tam giác DBM và tam giác FMB Có
góc BDM= góc BFM (=90)
BM chung(gt)
DBM=FMB (gt)
⇒ TAM GIÁC DMB \(\infty\)tam giác FMB
b)Theo a, ta có \(\Delta\) DBM = \(\Delta\) FMB( cạnh huyền- góc nhọn)
=> MD = BF (hai cạnh tương ứng) (*)
Ta có : FH \(\perp\) với AC(1)
ME \(\perp\) với AC(2)
Từ (1) và (2) \(\Rightarrow\): FH // ME
=> góc H1 = góc M3 (hai góc so le trong)
Xét\(\Delta\) MFH và \(\Delta\) HEM ta có:
HM: cạnh chung
Góc H1 = góc M3 (cmt)
\(\Rightarrow\) tam giác MFH = tam giác HEM (cạnh huyền - góc nhọn)
=>FH = ME (hai cạnh tương ứng) (**)
Từ (*) và (**) \(\Rightarrow\): MD + ME = BF + FH = BH
Suy ra : BH không đổi
=> MD + ME không đổi
C) Kẻ DN // AC cắt BC tại N,DK cắt BC tjai I CÓ góc DBN =góc C , góc C=DNB (đòng vị
\(\Rightarrow\) tam giác BDN cân tại D
\(\Rightarrow\)DB=DN
\(\Delta\) DBM= \(\Delta\) FMB ⇒ DB=MF
MF=HE=CK⇒BD=CK⇒DN=CK
⇒t\(\Delta\) DNI= \(\Delta\) KCI (g.c.g)
⇒ID=IK⇒I là trung điểm DK
Vậy,................................
#Châu's ngốc
 Vào thống kê hỏi đáp để lấy hình ảnh
Vào thống kê hỏi đáp để lấy hình ảnh