Trong không gian Oxyz cho điểm M(1;2;3). Phương trình mặt phẳng (P) đi qua M cắt các trục tọa độ Ox; Oy; Oz lần lượt tại A, B, C sao cho M là trong tâm của tam giác ABC là
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho điểm M(3;2;-1). Hình chiếu vuông góc của điểm M lên trục Oz là điểm:
A. M 3 3 ; 0 ; 0 .
B. M 4 0 ; 2 ; 0 .
C. M 1 0 ; 0 ; − 1 .
D. M 2 3 ; 2 ; 0 .
Đáp án C
M 1 ∈ O z ⇒ x M 1 = 0 ; y M 1 = 0 ; z M 1 = − 1
Trong không gian Oxyz, cho điểm M(3;2;-1). Hình chiếu vuông góc của điểm M lên trục Oz là điểm
A. M 3 3 ; 0 ; 0
A. M 4 0 ; 2 ; 0
C. M 1 0 ; 0 ; - 1
D. M 2 3 ; 2 ; 0
Đáp án C
M 1 ∈ O z ⇒ x M 1 = 0 ; y M 1 = 0 , z M 1 = - 1
Trong không gian Oxyz, cho điểm M(3;2;-1). Hình chiếu vuông góc của điểm M lên trục Oz là điểm:
A. M(3;0;0)
B. M(0;2;0)
C. M(0;0;-1)
D. M(3;2;0)
Trong không gian Oxyz, cho điểm M(3;2;-1) Hình chiếu vuông góc của điểm M lên trục Oz là điểm:
A. M 3 3 ; 0 ; 0
B. M 4 0 ; 2 ; 0
C. M 1 0 ; 0 ; - 1
D. M 2 3 ; 2 ; 0
Trong không gian Oxyz, cho điểm M(1;-2;5). Khoảng cách từ M đến trục Oz bằng
A. 5
B. 5
C. 1
D. 2
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A 1 ; 1 ; 1 , B 2 ; 0 ; - 1 . Điểm M trong không gian thỏa mãn M A = 2 M B . Khi đó độ dài OM nhỏ nhất bằng
A. 17 - 2 3
B. 19 + 2 3
C. 19 - 2 3
D. 2 3
Trong không gian Oxyz, cho điểm M(-2; 5; 1). Khoảng cách từ M đến trục Ox bằng:
A. √29
B. 2
C. √5
D. √26
Trong không gian Oxyz, cho điểm M(1;0;3) thuộc:
A. Mặt phẳng (Oxy)
B. Trục Oy
C. Mặt phẳng (Oyz)
D. Mặt phẳng (Oxz)
Đáp án D
Phương pháp: (Oxy): z = 0, (Oyz): x = 0, (Oxz): y = 0
Trục Oy: x = 0 y = t z = 0
Cách giải: M (1;0;3) ∈ (Oxz)
Trong không gian Oxyz, cho điểm M(1;0;3) thuộc:
A. Mặt phẳng (Oxy).
B. Trục Oy.
C. Mặt phẳng (Oyz).
D. Mặt phẳng (Oxz).
Trong không gian Oxyz, cho hai điểm A 1 ; 3 ; - 1 , B 3 ; - 1 ; 5 . Tìm tọa độ độ điểm M thỏa mãn M A → = 3 M B →
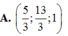
![]()
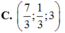
![]()