Cho hàm số f ( x ) có f ' ( x ) = x ( x - 3 ) 2 ( x - 2 ) 3 , ∀ x ∈ ℝ . Số điểm cực tiểu của hàm số đã cho là:
A. 3
B. 1
C. 5
D. 2
Bài 1: Xét tính đơn điệu của hàm số \(y=f(x)\) khi biết đạo hàm của hàm số là:
a) \(f'(x)=(x+1)(1-x^2)(2x-1)^3\)
b) \(f'(x)=(x+2)(x-3)^2(x-4)^3\)
Bài 2: Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x(x+1)(x-2)\). Xét tính biến thiên của hàm số:
a) \(y=f(2-3x)\)
b) \(y=f(x^2+1)\)
c) \(y=f(3x+1)\)
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = ( x + 1 ) ( x - 2 ) 2 ( x - 3 ) 3 ( x + 5 ) 4 . Hỏi hàm số y = f ( x ) có mấy điểm cực trị?
A. 2
B. 3
C. 4
D. 5
Chọn A
f ' ( x ) đổi dấu khi x chạy qua -1 và 3 nên hàm số có 2 điểm cực trị.
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị của hàm số f ' ( x ) , biết f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) và các khẳng định sau:
Hàm số y = f(x) có 2 điểm cực trị.
Hàm số y = f(x) đồng biến trên khoảng ( - ∞ ; 0 ) .
Max [ 0 ; 3 ] f ( x ) = f ( 3 ) .
Min ℝ f ( x ) = f ( 2 ) .
Max [ - ∞ ; 2 ] f ( x ) = f ( 0 ) .

Số khẳng định đúng là
A. 2.
B. 3.
C. 4.
C. 4.
Chọn C.
Dựa vào đồ thị hàm số f ' ( x ) suy ra BBT của hàm số y = f(x)

Khẳng định 1, 2, 5 đúng, khẳng định 4 sai.
Xét khẳng định 3: Ta có:
f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) ⇒ f ( 3 ) - f ( 0 ) = f ( 1 ) - f ( 2 ) > 0
Do đó f ( 3 ) > f ( 0 ) ⇒ Vậy khẳng định 3 đúng.
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = ( x + 1 ) 4 ( x - 2 ) 5 ( x + 3 ) 3 . Số điểm cực trị của hàm số f ( x ) là:
A. 5
B. 3
C. 1
D. 2
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = ( x + 1 ) 4 ( x - 2 ) 5 ( x + 3 ) 3 . Số điểm cực trị của hàm số f ( x ) là:
A. 5
B. 3
C. 1
D. 2
1) cho hàm số \(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}x^2+8x-1\) có đạo hàm là f'(x). Tập hợp những giá trị của x để f'(x) = 0
2) cho hàm số \(f\left(x\right)=\dfrac{3-3x+x^2}{x-1}\) giải bất phương trình f'(x) = 0
2: ĐKXĐ: x<>1
\(f'\left(x\right)=\dfrac{\left(x^2-3x+3\right)'\left(x-1\right)-\left(x^2-3x+3\right)\left(x-1\right)'}{\left(x-1\right)^2}\)
\(=\dfrac{\left(2x-3\right)\left(x-1\right)-\left(x^2-3x+3\right)}{\left(x-1\right)^2}\)
\(=\dfrac{2x^2-5x+3-x^2+3x-3}{\left(x-1\right)^2}=\dfrac{x^2-2x}{\left(x-1\right)^2}\)
f'(x)=0
=>x^2-2x=0
=>x(x-2)=0
=>\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
1:
\(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}\cdot x^2+8x-1\)
=>\(f'\left(x\right)=\dfrac{1}{3}\cdot3x^2-2\sqrt{2}\cdot2x+8=x^2-4\sqrt{2}\cdot x+8=\left(x-2\sqrt{2}\right)^2\)
f'(x)=0
=>\(\left(x-2\sqrt{2}\right)^2=0\)
=>\(x-2\sqrt{2}=0\)
=>\(x=2\sqrt{2}\)
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = ( x + 1 ) 2 ( x - 1 ) 3 ( 2 - x ) . Hàm số f ( x ) đồng biến trên khoảng nào dưới đây
![]()
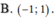
![]()
![]()
Cho f ( x ) có đạo hàm f ' ( x ) = x ( x + 1 ) 3 ( x - 2 ) 2 . Số điểm cực trị của hàm số f ( x ) là
A. 1
B. 2
C. 3
D. 6
Cho hàm số f(x) có đạo hàm f ’ ( x ) = ( x + 1 ) 2 ( x + 2 ) 3 ( 2 x - 3 ) . Tìm số điểm cực trị của f(x).
A. 3
B. 2
C. 0
D. 1
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = - 2017 ( x - 1 ) ( x + 2 ) 3 ( x - 3 ) 2 Tìm số điểm cực trị của f(x)
A. 3
B. 2
C. 0
D. 1
Đáp án B
Ta có y , = 0 ⇔ x = 1 x = - 2 x = 3 , y , đổi dấu qua x=1 và x=-2 , y , không đổi dấu qua x=3 nên hàm số có hai cực trị tại x=1 và x=-2