Gọi a là số thực lớn nhất để bất phương trình x 2 - x + 2 + a ln ( x 2 - x + 1 ) ≥ 0 nghiệm đúng với mọi x. Mệnh đề nào sau đây đúng?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Gọi a là số thực lớn nhất để bất phương trình x 2 - x + 2 + a ln x 2 - x + 1 ≥ 0 nghiệm đúng với mọi x ∈ ℝ . Mệnh đề nào sau đây đúng?
A. a ∈ ( 2 ; 3 ]
B. a ∈ 8 ; + ∞
C. a ∈ ( 6 ; 7 ]
D. a ∈ ( - 6 ; - 5 ]
Chọn đáp án C

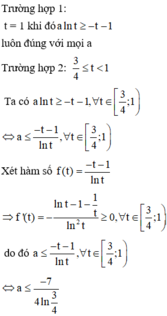
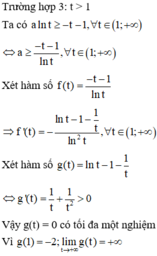
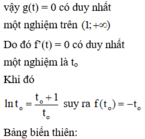
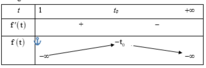

Vậy số thực a thỏa mãn yêu cầu bài toán là: a ∈ ( 6 ; 7 ]
Gọi a là số thực lớn nhất để bất phương trình x 2 − x − 2 + a ln x 2 − x + 1 ≥ 0 nghiệm đúng với mọi x ∈ ℝ . Mệnh đề nào sau đây đúng?
A. a ∈ 6 ; 7 .
B. a ∈ 2 ; 3 .
C. a ∈ − 6 ; − 5 .
D. a ∈ 8 ; + ∞
Đáp án A.
Đặt t = x 2 − x + 1 = x − 1 2 2 + 3 4 ≥ 3 4
Khi đó BPT trở thành
f t = t + 1 + a ln t ≥ 0
Ta có: f ' t = + ∞ ; f 3 4 = 3 4 + a ln 3 4
Với a > 0 ⇒ f t đồng biến trên
3 4 ; + ∞ ⇒ f t ≥ 0 ∀ t ∈ 3 4 ; + ∞ ⇔ M i n 3 4 ; + ∞ f t = 7 4 + a
⇔ a ln 3 4 ≥ − 7 4 ⇔ a ≤ − 7 4 ln 3 4 ≈ 6 , 08.
Vì đề bài yêu cầu tìm số thực lớn nhất
nên suy ra a ∈ 6 ; 7 .
Gọi a là số thực lớn nhất để bất phương trình x 2 − x + 2 + a ln x 2 − x + 1 ≥ 0 nghiệm đúng với mọi x ∈ ℝ . Mệnh đề nào sau đây đúng?
A. a ∈ 6 ; 7
B. a ∈ 2 ; 3
C. a ∈ − 6 ; − 5
D. a ∈ 8 ; + ∞
Gọi a là số thực lớn nhất để bất phương trình x 2 - x + 2 + a ln ( x 2 - x + 1 ) ≥ 0 nghiệm đúng với mọi x ∈ R . Mệnh đề nào sau đây đúng?
A. a ∈ ( 8 ; + ∞ )
B. a ∈ ( - 6 ; - 5 )
C. a ∈ ( 6 ; 7 )
D. a ∈ ( 2 ; 3 )
Có bao nhiêu số nguyên a ∈ ( - 200 ; 200 ) để phương trình e x + e x + a = ln ( 1 + x ) - ln ( x + a + 1 ) có nghiệm thực duy nhất.
A. 399
B. 199
C. 200
D. 398
Biết rằng m là một số dương để bất phương trình m x ≥ 2 x + 1 nghiệm đúng với ∀ x ∈ ℝ . Giá trị lớn nhất của hàm số y = x + ln m x - 1 , x ∈ 2 ; 4 thuộc đoạn nào dưới đây
A. [1;2]
B. [2,5;5]
C. [5;6]
D. [7;9]
4) Tìm a thuộc Z để phương trình sau có nghiệm duy nhất là số nguyên
a^2x+2x=3(a+1-ax)
5) Tìm m để phương trình: (m^2+5)x=2-2mx
có nghiệm duy nhất đạt giá trị lớn nhất
6) Tìm tất cả các số thực a không âm sao cho phương trình: (a^2-4)x=a^2-ma+16 (ẩn x)
có nghiệm duy nhất là số nguyên
1.Bất phương trình (m2-3m)x+m<2-2x vô nghiệm khi:
a.m#1 b.m#2 c.m=2 d.=3
2.Gọi S là tập hợp tất cả các giá trị thực của tham số m để bất phương trình (m2-m)x +m<6x-2
GIUP MÌNH VỚI Ạ
Câu 2 bạn ghi thiếu đề
Câu 1:
\(\Leftrightarrow\left(m^2-3m\right)x+2x< 2-m\)
\(\Leftrightarrow\left(m^2-3m+2\right)x< 2-m\)
BPT đã cho vô nghiệm khi và chỉ khi:
\(\left\{{}\begin{matrix}m^2-3m+2=0\\2-m\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=1\\m=2\end{matrix}\right.\\m\ge2\end{matrix}\right.\) \(\Rightarrow m=2\)
Tập hợp các số thực m để phương trình ln x 2 - m x - 2019 = ln x có nghiệm duy nhất là
A. ∅
B. - 1
C. 0
D. ℝ
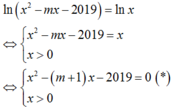
Nhận thấy phương trình (*) có a c < 0 ⇒ * có 2 nghiệm phân biệt, do đó ∀ m ∈ ℝ phương trình (*) luôn có 1 nghiệm thỏa mãn x > 0 .
Chọn D.