Cho hàm số f ( x )   =   tan x   ( 2 c o t x -   2 cos x   +   cos 2 x )  có nguyên hàm là F(x) và F π 4 =   π 2  . Giả sử F ( x )   =   a x   +   b cos x   -   cos   c x 2   - d  . Chọn phát biểu đúng.

Nguyên hàm của hàm số f ( x ) = cos ( 5 x - 2 )   là.

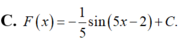
Hàm số f ( x ) = cos   x sin 5   x  có một nguyên hàm F(x) bằng

A.  1 8 sin 4 x

B.  - 1 8 sin 4 x + 1

C.  4 sin 4 x

D.  - 1 4 sin 4 x + 2

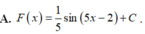
Hàm số F(x) = ln|sin x – cos x| là một nguyên hàm của hàm số

A.  f ( x ) = sin x + cos x sin x - cos x

B.  f ( x ) = sin x - cos x sin x + cos x

C.  f ( x ) = 1 sin x + cos x

D.  f ( x ) = 1 sin x - cos x

xét hàm số y = f(x) = \(\cos\frac{x}{2}\).

a) chứng minh rằng với mỗi số nguyên k , f\(\left(x+k4\pi\right)\)=f(x) với mọi x .

b) lập bảng biến thiên của hàm số y = \(\cos\frac{x}{2}\) trên đoạn \(\left[-2\pi;2\pi\right]\).

c) vẽ đồ thị các hàm số y = \(\cos x\) và y = \(\cos\frac{x}{2}\) trong cùng một hệ tọa độ vuông góc Oxy .

d) trong mặt phẳng tọa độ Oxy , xét phép biến hình F biến mỗi điểm (x ; y) thành (x' ; y') sao cho x'=2x và y'=y . chứng minh rằng F biến đồ thị hàm số y = \(\cos x\) thành đồ thị hàm số y = \(\cos\frac{x}{2}\) .

Cho hàm số    f x = tan   x 2 c o t   x + 2 cos   x + 2 cos 2 x có

nguyên hàm là F(x)  và  F π 4 = π 2 .

Giả sử  F x = a x + b cos x - cos   c x 2 - d  .Chọn phát biểu

đúng:

A. a : b : c = 1 : 2 : 1

B. a + b + c = 6

C. a + b = 3c

D. a – b +  c = d