Cho hình lăng trụ A B C . A ' B ' C ' có thể tích là V . Điểm M nằm trên cạnh A A ' sao cho A M = 2 M A ' . Gọi V ' là thể tích của khối chóp M . B C C ' B ' M.BCC’B’. Tính tỉ số V ' V .
A. V ' V = 1 3
B. V ' V = 1 2
C. V ' V = 3 4
D. V ' V = 2 3
Cho lăng trụ tam giác ABC.A′B′C′. Gọi M,N,P lần lượt là trung điểm các cạnh A′B′,BC,CC′. Mặt phẳng (MNP) chia khối lăng trụ thành hai phần, phần chưa điểm B có thể tích là V 1 . Gọi V là thể tích khối lăng trụ. Tính V 1 V .
A. 25 288
B. 29 144
C. 37 288
D. 19 144
Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi, AC=2a, BAD= 120 o Hình chiếu vuông góc của điểm B trên mặt phẳng (A'B'C'D') là trung điểm cạnh A' B' góc giữa mặt phẳng (AC'D') và mặt đáy lăng trụ bằng 60 o . Tính thể tích V của khối lăng trụ ABCD.A'B'C'D'?
![]()
![]()
![]()
![]()
Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi, A C = 2 a , B A D ^ = 120 ∘ . Hình chiếu vuông góc của điểm B trên mặt phẳng A ' B ' C ' D ' là trung điểm cạnh A' B' góc giữa mặt phẳng A C ' D ' và mặt đáy lăng trụ bằng 60 ∘ . Tính thể tích V của khối lăng trụ A B C D . A ' B ' C ' D '
A. V = 2 3 a 3
B. V = 3 3 a 3
C. V = 3 a 3
D. V = 6 3 a 3
Đáp án D
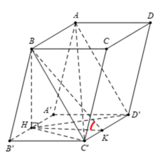
Gọi H là trung điểm của BC, kẻ H K ⊥ C ' D ' K ∈ C ' D '
Suy ra B H ⊥ A ' B ' C ' D ' ⇒ A C ' D ' ; A ' B ' C ' D ' ^ = B K H ^
Tam giác A’C’D’ đều cạnh 2 a ⇒ H K = d A ' ; C ' D ' = a 3
Tam giác BHK vuông tại H ⇒ B H = tan 60 ∘ x H K = 3 a
Diện tích hình thoi A’B’C’D’ là S A ' B ' C ' D ' = 2 a 2 3 .
Vậy thể tích khối lăng trụ ABC.A’B’C’D’ là V = B H . S A ' B ' C ' D ' = 3 a .2 a 2 3 = 6 3 a 3
cho hình lăng trụ tam giác đều ABC.A'B'C' có chín cạnh đều bằng a
a, tính diện tích toàn phần và thể tích hình lăng trụ theo a
b, gọi M là điểm di động trên cạnh A'B' (M không trùng B'). mặt phẳng ( MBC) cắt đường thẳng A'C' tại N. chứng minh tứ giác BMNC là hình thang cân
c, gọi I,J lần lượt là giao điểm của các cặp đường thẳng BM và CN,BN,CM. chứng minh I,J lần lượt nằm trên đường thẳng cố định khi M di động . chỉ rõ 2 đường thẳng đó
Cho hình lăng trụ đứng ABC.A′B′C′ có đáy là tam giác đều cạnh a. Cạnh bên BB′=b. Thể tích của khối lăng trụ ABC.A′B′C′ là
A. a 3 b 3
B. a 2 b 3 4
C. a 2 b 3
D. a 3 b 3 3
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có góc giữa hai mặt phẳng (A′BC) và (ABC) bằng 60 0 , cạnh AB = 2. Thể tích V của khối lăng trụ ABC.A′B′C′ là
A. 3 3 4
B. 3
C. 3
D. 3 3
Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh cùng bằng a, hình chiếu của C trên mặt phẳng (ABB’A’) là tâm của hình bình hành ABB’A’. Tính theo a thể tích khối cầu đi qua năm điểm A, B, B’, A’ và C
A. π 2 a 3 3
B. 8 π 2 a 3 81
C. π 2 a 3 24
D. π 2 a 3 81
Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh cùng bằng a, hình chiếu của C trên mặt phẳng (ABB’A’) là tâm của hình bình hành ABB’A’. Tính theo a thể tích khối cầu đi qua năm điểm A, B, B’, A’ và C.
A. π 2 a 3 3
B. 8 π 2 a 3 81
C. π 2 a 3 24
D. π 2 a 3 81
Đáp án A
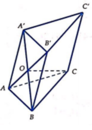
Gọi O là tâm hình bình hành A B B ' A ' , ta có C O ⊥ A B B ' A ' .
Vì C A = C B nên O A = O B , suy ra hình thoi A B B ' A ' là hình vuông.
Do đó O A = A B 2 = a 2 . Suy ra O C 2 = A C 2 − A O 2 = a 2 2 ⇒ O C = a 2
Suy ra tam giác ABC vuông tại C. Từ đây ra suy ra khối caauff đi qua năm điểm A ; B ; B ' ; A ' và C là khối cầu tâm O bán kính O A = a 2 .
Vậy thể tích khối cầu là V = 4 3 π . O A 3 = π 2 a 3 3
Cho hình lăng trụ đứng ABCD.A′B′C′D′ có đáy là hình vuông cạnh bằng 4cm, đường chéo AB′ của mặt bên (ABB′A′) có độ dài bằng 5cm. Tính thể tích V của khối lăng trụ ABCD.A′B′C′D′.
A. 48 cm 3
B. 24 cm 3
C. 16 cm 3
D. 32 cm 3