Đáp án A
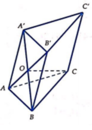
Gọi O là tâm hình bình hành A B B ' A ' , ta có C O ⊥ A B B ' A ' .
Vì C A = C B nên O A = O B , suy ra hình thoi A B B ' A ' là hình vuông.
Do đó O A = A B 2 = a 2 . Suy ra O C 2 = A C 2 − A O 2 = a 2 2 ⇒ O C = a 2
Suy ra tam giác ABC vuông tại C. Từ đây ra suy ra khối caauff đi qua năm điểm A ; B ; B ' ; A ' và C là khối cầu tâm O bán kính O A = a 2 .
Vậy thể tích khối cầu là V = 4 3 π . O A 3 = π 2 a 3 3