Tập xác định của hàm số y = x 2 - 3 x + 2 π là:
A . ( - ∞ ; 1 ) ∪ ( 2 ; + ∞ )
B . ℝ
C . ( 0 ; + ∞ )
D . ( 1 ; 2 )
Tập xác định của hàm số y = x 2 - 3 x + 2 3 5 + x - 3 - 2 là
A . D = ( - ∞ ; + ∞ ) \ { 3 }
B . D = ( - ∞ ; 1 ) ∪ ( 2 ; + ∞ ) \ { 3 }
C . D = ( - ∞ ; + ∞ ) \ ( 1 ; 2 )
D . D = ( - ∞ ; 1 ) ∪ ( 2 ; + ∞ )
Chọn B
Hàm số xác định khi và chỉ khi
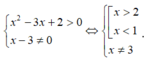
Vậy tập xác định ![]()
Tập xác định của hàm số y = x 2 - 3 x + 2 3 5 + x - 3 - 2 là
A. D= ( - ∞ ; + ∞ ) \ { 3 }
B. D = ( - ∞ ; 1 ) ∪ ( 2 ; + ∞ ) \ { 3 }
C. D = ( - ∞ ; + ∞ ) \ ( 1 ; 2 )
D. D = ( - ∞ ; 1 ) ∪ ( 2 ; + ∞ )
Tập xác định D của hàm số
y = ( x 2 - 3 x + 2 ) 3 5 + ( x - 3 ) - 2 là
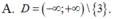
![]()
![]()
![]()
Tập xác định của hàm số y = 2 x - 3 + 4 x - 3 là:
A. D = 3 2 ; 4 3
B. D = 2 3 ; 3 4
C. D = 4 3 ; 2 3
D. D = [ 3 2 ; + ∞ )
Điều kiện xác định: 2 x - 3 ≥ 0 4 x - 3 ≥ 0 ⇔ x ≥ 3 2 x ≥ 3 4 ⇔ x ≥ 3 2
Tập xác định của hàm số là [ 3 2 ; + ∞ )
Giá trị nhỏ nhất của hàm số \(y=\sqrt{4-x}+\sqrt{3}\) trên tập xác định của nó là
A: 2 + \(\sqrt{3}\)
B: 2\(\sqrt{3}\)
C: 0
D: \(\sqrt{3}\)
\(\sqrt{4-x}\ge0\) với mọi x thuộc TXĐ nên \(y=\sqrt{4-x}+\sqrt{3}\ge\sqrt{3}\)
Đáp án D
Tập xác định của hàm số y = 4 x - 3 + 5 x - 6 là:
A. D = 6 5 ; + ∞
B. D = [ 6 5 ; + ∞ )
C. D = [ 3 4 ; + ∞ )
D. D = 3 4 ; 6 5
Điều kiện xác định: 4 x - 3 ≥ 0 5 x - 6 ≥ 0 ⇔ x ≥ 3 4 x ≥ 6 5 ⇔ x ≥ 6 5
Tập xác định của hàm số là D = [ 6 5 ; + ∞ ) .
Tìm điều kiện cần và đủ của tham số m để tập xác định của hàm số y = m - 2 x - x + 1 là một đoạn trên trục số.
A. m < - 2
B. m > 2
C. m > - 1 2
D. m > - 2
Hàm số y = m - 2 x - x + 1 xác định khi và chỉ khi m - 2 x ≥ 0 x + 1 ≥ 0 ⇔ x ≤ m 2 x ≥ - 1 .
Do đó tập xác định của hàm số y = m - 2 x - x + 1 là một đoạn trên trục số khi và chỉ khi m 2 > - 1 ⇔ m > - 2
Tập xác định D của hàm số y = ( x 2 - 3 x + 2 ) π
![]()
![]()
![]()
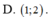
Tập xác định của hàm số y = tan 2 x là:
![]()

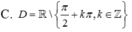
![]()
Tập xác định của hàm số y = tan 2 x là:
A. D = ℝ \ π 4 + k π ; k ∈ ℤ
B. D = ℝ \ π 4 + k π 2 ; k ∈ ℤ
C. D = ℝ \ π 2 + k π ; k ∈ ℤ
D. D = ℝ \ k π 2 ; k ∈ ℤ