Một con lắc lò xo nằm ngang dao động theo phương trình x = 5 cos 2 πt - π 3 (x tính bằng cm; t tính bằng s). Kể từ t = 0 , lò xo không biến dạng lần đầu tại thời điểm
A. 5/12 s.
B. 1/6 s.
C. 2/ 3s.
D. 11/12s.
1. Con lắc lò xo là gì? Viết các công thức tính tần số góc, chu kì, tần số của con lắc lò xo.
2. Viết các biểu thức tính động năng, thế năng, cơ năng của con lắc lò xo.
3. Vận dụng: Một CLLX dao động theo phương nằm ngang với phương trình
\(x=8cos4\pi t\) (cm). Biết \(m=200\) g. Tính thế năng của con lắc khi lực đàn hồi \(F=1,92\) N.
1.Con lắc lò xo gồm một vật nhỏ có khối lượng m gắn vào đầu một lò xo có độ cứng k và khối lượng không đáng kể.
Từ \(\Delta\)\(l_{0}.k\)\(=mg\)
\(T=2\)\(\pi\)\(\sqrt{\dfrac{m}{k}}\)\(=\dfrac{t}{N}(s)\)
\(f=\dfrac{1}{2π} \)\(\sqrt{\dfrac{k}{m}}\)\(=\dfrac{N}{t}(Hz)\)
\(\omega\)\(=\sqrt{\dfrac{k}{m}}=\)\(\dfrac{2π}{T}=2πf\)
2.
- Động năng của con lắc lò xo:
- Thế năng đàn hồi của con lắc lò:
- Trong con lắc lò xo nằm ngang x = ∆l nên:
- Cơ năng trong con lắc lò xo:
3.Ta có \(F=kx=1,92N\)
\(\omega\)=\(4\)\(\pi\) ;\(m=0,2(kg)\)
\(\Rightarrow\)\(k=m.\)\(\omega\).\(\omega\)=\(32(N/m)\)
\(\Rightarrow\)\(x=0,06\)
\(W_{t}=\dfrac{1}{2}.k.x^{2}=0,0576(J)\)
1.Con lắc lò xo là một hệ thống bao gồm 1 lò xo có độ cứng là k, tạm thời bỏ qua ảnh hưởng của khối lượng (điều kiện lý tưởng): một đầu cố định, một đầu gắn vật nặng có khối lượng m (bỏ qua sự ảnh hưởng của kích thước).
CT tính tần số góc:\(\omega=\sqrt{\dfrac{k}{m}}\)
CT tính chu kì:\(T=2\pi\sqrt{\dfrac{m}{k}}\)
CT tính tần số:\(f=\dfrac{1}{2\pi}\sqrt{\dfrac{k}{m}}\)
2.Biểu thức tính:
+ Động năng:\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}mA^2sin^2\left(\omega t+\varphi\right)\)
+ Thế năng: \(W_t=\dfrac{1}{2}kx^2=\dfrac{1}{2}kA^2cos^2\left(\omega t+\varphi\right)\)
+ Cơ năng: \(W=W_đ+W_t\)
Một con lắc lò xo nằm ngang dao động theo phương trình
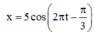
(x tính bằng cm; t tính bằng s). Kể từ , lò xo không biến dạng lần đầu tại thời điểm
A. 5/12 s
B.1/6 s
C.2/3 s
11/12 s
Đáp án A
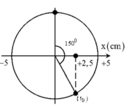
Lò xo nằm ngang không biến dạng khi vật đi qua vtcb (x = 0).
Góc quay từ t = 0 đến x = 0 lần đầu tiên
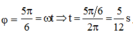
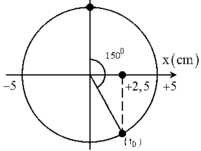
Một con lắc lò xo nằm ngang dao động theo phương trình x = 5 cos 2 π t − π 3 (x tính bằng cm; t tính bằng s). Kể từ t = 0 , lò xo không biến dạng lần đầu tại thời điểm
A. 5 12 s
B. 1 6 s
C. 2 3 s
D. 11 12 s
Đáp án A
Lò xo nằm ngang không biến dạng khi vật đi qua vtcb (x = 0)
Góc quay từ t = 0 đến x = 0 lần đầu tiên: φ = 5 π 6 = ω t ⇒ t = 5 π / 6 2 π = 5 12 s
Một con lắc lò xo nằm ngang dao động theo phương trình x = 5 cos 2 π t - π 3 (x tính bằng cm; t tính bằng s). Kể từ t = 0, lò xo không biến dạng lần đầu tại thời điểm
A. 5 12 s
B. 1 6 s
C. 2 3 s
D. 11 12 s
Chọn đáp án A
Lò xo không biến dạng tại vị trí cân bằng.
→ Biểu diễn dao động của vật tương ứng trên đường tròn.
Từ hình vẽ ta thấy rằng khoảng thời gian tương ứng là
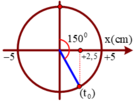
Một con lắc lò xo nằm ngang dao động theo phương trình x = 5 cos 2 πt - π 3 (x tính bằng cm; t tính bằng s). Kể từ t=0 , lò xo không biến dạng lần đầu tại thời điểm
A. 5/12 s
B. 1/6 s
C. 2/3 s
D. 11/12 s
+ Lò xo không biến dạng tại vị trí cân bằng.
→ Biểu diễn dao động của vật tương ứng trên đường tròn.
+ Từ hình vẽ ta thấy rằng khoảng thời gian tương ứng là 5/12 s → Đáp án A
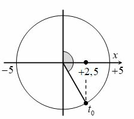
Một con lắc lò xo nằm ngang dao động theo phương trình x = 5 cos 2 π t − π 3 (x tính bằng cm; t tính bằng s). Kể từ t=0, lò xo không biến dạng lần đầu tại thời điểm
A. 5 12 s
B. 1 6 s
C. 2 3 s
D. 11 12 s
Chọn đáp án A
Lò xo không biến dạng tại vị trí cân bằng.
→ Biểu diễn dao động của vật tương ứng trên đường tròn.
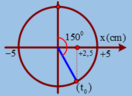
Từ hình vẽ ta thấy rằng khoảng thời gian tương ứng là t = 5 12 T = 5 12 s
Một con lắc lò xo nằm ngang dao động điều hòa với phương trình x=5cos(10πt+π/3)cm. Chiều dài tự nhiên của lò xo là 20cm. Tính lmax,lmin của lò xo trong quá trình vật dao động.
\(l_{max}=l_0+\Delta l+A\Rightarrow\left\{{}\begin{matrix}A=5cm=0,02m\\\Delta l=\dfrac{g}{\omega^2}=\dfrac{10}{\left(10\right)^2}=0,1m\\l_0=0,2m\end{matrix}\right.\)
=> \(l_{max}=0,2+0,1+0,02=0,32\left(m\right)=32cm\)
\(l_{min}=l_0+\Delta l-A=0,2+0,1-0,02=0,28\left(m\right)=28\left(cm\right)\)
Vậy ...
Một con lắc lò xo nằm ngang dao động theo phương trình x = 5cos(2πt – π/3) (x tính bằng cm; t tính bằng s). Kể từ t = 0, lò xo không biến dạng lần đầu tại thời điểm
A. 5/12 s
B. 1/6 s
C. 2/3 s
D. 11/12 s
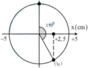
Lò xo không biến dạng tại vị trí cân bằng.
→ Biểu diễn dao động của vật tương ứng trên đường tròn.
Từ hình vẽ ta thấy rằng khoảng thời gian tương ứng là t = 5T/12 = 5/12
Đáp án A
Một con lắc lò xo gồm lò xo và vật nhỏ dao động điều hòa theo phương nằm ngang. Động năng của con lắc đạt giá trị cực tiểu khi
A. lò xo có chiều dài cực đại.
B. lò xo không biến dạng.
C. vật có vận tốc cực đại.
D. vật đi qua vị trí cân bằng.
+ Động năng của con lắc cực tiểu tại vị trí biên
→ chiều dài lò xo cực đại.
Đáp án A