Hãy xác định các hệ số a, b, c để hàm số y = a x 4 + b x 2 + c có đồ thị như hình vẽ
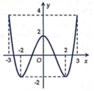
A. a = − 4, b = − 2, c = 2.
B. a = 1 4 , b = − 2, c = 2.
C. a = 4, b = 2, c = − 2.
D. a = 1 4 , b = 2, c = 2.
Cho hàm số bậc hai \(y = f(x) = a{x^2} + bx + c\) có \(f(0) = 1,f(1) = 2,f(2) = 5.\)
a) Hãy xác định giá trị của các hệ số \(a,b\) và \(c.\)
b) Xác định tập giá trị và khoảng biến thiên của hàm số.
Tham khảo:
a) Ta có: \(f(0) = a{.0^2} + b.0 + c = 1 \Rightarrow c = 1.\)
Lại có:
\(f(1) = a{.1^2} + b.1 + c = 2 \Rightarrow a + b + 1 = 2\)
\(f(2) = a{.2^2} + b.2 + c = 5 \Rightarrow 4a + 2b + 1 = 5\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}a + b + 1 = 2\\4a + 2b + 1 = 5\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a + b = 1\\4a + 2b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\)(thỏa mãn điều kiện \(a \ne 0\))
Vậy hàm số bậc hai đó là \(y = f(x) = {x^2} + 1\)
b) Tập giá trị \(T = \{ {x^2} + 1|x \in \mathbb{R}\} \)
Vì \({x^2} + 1 \ge 1\;\forall x \in \mathbb{R}\) nên \(T = [1; + \infty )\)
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.1}} = 0;{y_S} = f(0) = 1\)
Hay \(S\left( {0;1} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:

Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
Cho hàm số \(y = (x - 1)(2 - 3x)\)
a) Hàm số đã cho có phải hàm số bậc hai không? Nếu có, hãy xác định các hệ số a, b, c của nó.
b) Thay dấu “?” bằng các số thích hợp để hoàn thành bảng giá trị sau của hàm số đã cho.
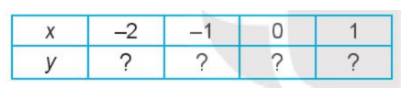
a) Ta có \((x - 1)(2 - 3x) = 2x - 3{x^2} - 2 + 3x = - 3{x^2} + 5x - 2\)
Do đó hàm y=(x-1)(2-3x) là hàm số bậc hai với \(a = - 3;b = 5;c = - 2\)
b) Thay các giá trị của x vào y = (x - 1)(2 - 3x) ta có:

Bài 1: Tìm m để các hàm số sau là hàm số bậc nhất
a) y= ( m - 2 )x - \(\dfrac{2}{3}\) b) y= ( 4 - 2022m )x - 2 c) y= \(\sqrt{1-2m}\)x + m - 3
Bài 2: Cho đồ thị hàm số y= -2x + 3
a) Xác định hệ số a,b
b) Các điểm A( -2 ; 7) ; B(\(\sqrt{2}\) ; 6)
c) Tìm tọa độ điểm M thuộc ( d ) có tung độ = 11
d) Tìm tọa độ điểm C thuộc ( d ), biết rằng hoành độ của điểm C gấp 3 tung độ của nó
e) Tìm tọa độ điểm E thuộc ( d ), biết rằng tung độ của điểm E và hoành độ là 2 số đối nhau
Xác định các hệ số a b c để hàm số y=ax2+bx+c có giá trị nhỏ nhất bằng 3/4 khi x=1/2 và nhận giá trị bằng 1 khi x =1
Hãy xác định các hệ số a, b, c để hàm số y = a x 4 + b x 2 + c có đồ thị như hình vẽ
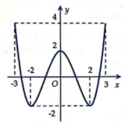
A. a = − 4 , b = − 2 , c = 2.
B. a = 1 4 , b = − 2 , c = 2.
C. a = 4 , b = 2 , c = − 2.
D. a = 1 4 , b = 2 , c = 2.
trong các hàm số sau hàm số nào là hàm số bậc nhất hãy xác định các hệ số a,b
a) y= 2x 2 + 3x+1/ x
b) (2x-3)(x-3)-2x2
c) -x-1/ 4
\(y=\frac{2x^2+3x+1}{x}\)
hàm số ko phải là hàm bậc nhất
\(b,y=\left(2x-3\right)\left(x-3\right)-2x^2\)
\(y=2x^2-3x-6x+9-2x^2\)
\(y=9-9x< =>\)hàm số là hàm bậc nhất
\(a=-9,b=9\)
\(c,y=-x-\frac{1}{4}\)<=> hàm số là hàm bậc nhất
\(a=-1;b=-\frac{1}{4}\)
Cho các hàm số bậc nhất hãy xác định hệ số a,b của chúng:
y = -3x + 2 (a = ... ; b = ...)
y = 5x (a = ... ; b = ...)
y = 1 + 4 (a = ... ; b = ...)
C2:
vẽ đồ thị các hàm số sau:
a. y= 2x + 1
b. y = -x + 2
Câu 1:
y=-3x+2
a=-3; b=2
y=5x
a=5; b=0
1,hãy xác định các hệ số a,b,c của hàm số f(x)=ax^2+bx+c biết rằng f(0)=1, f(1)=2, f(2)=2
2, vẽ đồ thị hàm số y=-2x. tìm trên đồ thị những điểm có tung độ =-1,2,-4
Trong các hàm số sau, hàm số nào là hàm số bậc hai? Với những hàm số bậc hai đó, xác định \(a,b,c\) lần lượt là hệ số của \({x^2}\), hệ số của \(x\) và hệ số tự do.
a) \(y = - 3{x^2}\)
b) \(y = 2x\left( {{x^2} - 6x + 1} \right)\)
c) \(y = 4x\left( {2x - 5} \right)\)
a) Hàm số \(y = - 3{x^2}\) là hàm số bậc hai.
\(y = - 3.{x^2} + 0.x + 0\)
Hệ số \(a = - 3,b = 0,c = 0\).
b) Hàm số \(y = 2x\left( {{x^2} - 6x + 1} \right)\)\( \Leftrightarrow y = 2{x^3} - 12{x^2} + 2x\) có số mũ cao nhất là 3 nên không là hàm số bậc hai.
c) Hàm số \(y = 4x\left( {2x - 5} \right)\)\( \Leftrightarrow y = 8{x^2} - 20x\) có số mũ cao nhất là 2 nên là hàm số bậc hai.
Hệ số \(a = 8,b = - 20,c = 0\)