Cho (P): x - y - z - 3 = 0, d : x - 2 = 4 3 = z 5 . Gọi A = d ∩ P và M là trung điểm OA. Tính khoảng cách h từ M tới (P):
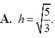
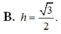
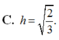
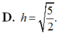
ìm x,y,z thuộc Q:
a)|x+9/2|+|y+4/3|+|z+7/2| nhỏ hơn hoặc bằng 0
b)|x+3/4|+|y-2/5|+|z+1/2| nhỏ hơn hoặc bằng 0
c) |x+19/5|+|y+1890/1975|+|z-2004|=0
d) |x+3/4|+|y-1/5|+|x+y+z|=0
a,
\(\left|x+\dfrac{9}{2}\right|\ge0\forall x\\ \left|y+\dfrac{4}{3}\right|\ge0\forall y\\ \left|z+\dfrac{7}{2}\right|\ge0\forall z\\ \Rightarrow\left|x+\dfrac{9}{2}\right|+\left|y+\dfrac{4}{3}\right|+\left|z+\dfrac{7}{2}\right|\ge0\forall x,y,z\)
Mà
\(\left|x+\dfrac{9}{2}\right|+\left|y+\dfrac{4}{3}\right|+\left|z+\dfrac{7}{2}\right|\le0\\ \Rightarrow\left|x+\dfrac{9}{2}\right|+\left|y+\dfrac{4}{3}\right|+\left|z+\dfrac{7}{2}\right|=0\\ \Rightarrow\left\{{}\begin{matrix}\left|x+\dfrac{9}{2}\right|=0\\\left|y+\dfrac{4}{3}\right|=0\\\left|z+\dfrac{7}{2}\right|=0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x+\dfrac{9}{2}=0\\y+\dfrac{4}{3}=0\\z+\dfrac{7}{2}=0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x=\dfrac{-9}{2}\\y=\dfrac{-4}{3}\\z=\dfrac{-7}{2}\end{matrix}\right.\)
Vậy \(x=\dfrac{-9}{2};y=\dfrac{-4}{3};z=\dfrac{-7}{2}\)
d,
\(\left|x+\dfrac{3}{4}\right|\ge0\forall x\\ \left|y-\dfrac{1}{5}\right|\ge0\forall y\\ \left|x+y+z\right|\ge0\forall x,y,z\\ \Rightarrow\left|x+\dfrac{3}{4}\right|+\left|y-\dfrac{1}{5}\right|+\left|x+y+z\right|\ge0\forall x,y,z\)
Mà
\(\left|x+\dfrac{3}{4}\right|+\left|y-\dfrac{1}{5}\right|+\left|x+y+z\right|=0\\ \Rightarrow\left\{{}\begin{matrix}\left|x+\dfrac{3}{4}\right|=0\\\left|y-\dfrac{1}{5}\right|=0\\\left|x+y+z\right|=0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x+\dfrac{3}{4}=0\\y-\dfrac{1}{5}=0\\x+y+z=0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x=\dfrac{-3}{4}\\y=\dfrac{1}{5}\\x+y+z=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-3}{4}\\y=\dfrac{1}{5}\\\dfrac{-3}{4}+\dfrac{1}{5}+z=0\end{matrix}\right.\\\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-3}{4}\\y=\dfrac{1}{5}\\\dfrac{-11}{20}+z=0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x=\dfrac{-3}{4}\\y=\dfrac{1}{5}\\z=\dfrac{11}{20}\end{matrix}\right.\)
b,
\(\left|x+\dfrac{3}{4}\right|\ge0\forall x\\ \left|y-\dfrac{2}{5}\right|\ge0\forall y\\ \left|z+\dfrac{1}{2}\right|\ge0\forall z\\ \Rightarrow\left|x+\dfrac{3}{4}\right|+\left|y-\dfrac{2}{5}\right|+\left|z+\dfrac{1}{2}\right|\ge0\forall x,y,z\\ \)
Mà \(\left|x+\dfrac{3}{4}\right|+\left|y-\dfrac{2}{5}\right|+\left|z+\dfrac{1}{2}\right|\le0\\ \Rightarrow\left|x+\dfrac{3}{4}\right|+\left|y-\dfrac{2}{5}\right|+\left|z+\dfrac{1}{2}\right|=0\\ \Rightarrow\left\{{}\begin{matrix}\left|x+\dfrac{3}{4}\right|=0\\\left|y-\dfrac{2}{5}\right|=0\\\left|z+\dfrac{1}{2}\right|=0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x+\dfrac{3}{4}=0\\y-\dfrac{2}{5}=0\\z+\dfrac{1}{2}=0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x=\dfrac{-3}{4}\\y=\dfrac{2}{5}\\z=\dfrac{-1}{2}\end{matrix}\right.\)
Vậy ...
c,
\(\left|x+\dfrac{19}{5}\right|\ge0\forall x\\ \left|y+\dfrac{1890}{1975}\right|\ge0\forall y\\ \left|z-2004\right|\ge0\forall z\\ \Rightarrow\left|x+\dfrac{19}{5}\right|+\left|y+\dfrac{1890}{1975}\right|+\left|z-2004\right|\ge0\forall x,y,z\)
Mà
\(\left|x+\dfrac{19}{5}\right|+\left|y+\dfrac{1890}{1975}\right|+\left|z-2004\right|=0\\ \Rightarrow\left\{{}\begin{matrix}\left|x+\dfrac{19}{5}\right|=0\\\left|y+\dfrac{1890}{1975}\right|=0\\\left|z-2004\right|=0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x+\dfrac{19}{5}=0\\y+\dfrac{1890}{1975}=0\\z-2004=0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x=\dfrac{-19}{5}\\y=\dfrac{-1890}{1975}=\dfrac{-378}{395}\\z=2004\end{matrix}\right. \)
Vậy ...
Tìm x ,y ,z biet :
a, |x+3/4|+|y-1/5|+|x+y+z|=0
b, |3x-4|+|3y-5|=0
c,|x+3/4|+|y-2/5|+|z+1/2| <0
d, |x+1/5|+|3-y|=0
a) \(|x+\frac{3}{4}|+|y-\frac{1}{5}|+|x+y+z|=0\)
\(\Rightarrow|x+\frac{3}{4}|=|y-\frac{1}{5}|=|x+y+z|=0\)
\(\Rightarrow|x+\frac{3}{4}|=0\) \(\Rightarrow|y-\frac{1}{5}|=0\) \(\Rightarrow|x+y+z|=0\)
\(\Rightarrow x+\frac{3}{4}=0\) \(\Rightarrow y-\frac{1}{5}=0\) \(\Rightarrow x+y+z=0\)
\(x=\frac{-3}{4}\) \(y=\frac{1}{5}\) thay x=-3/4; y=1/5 vào biểu thức trên
ta có \(\frac{-3}{4}+\frac{1}{5}+z=0\)
\(z=0-\frac{-3}{4}-\frac{1}{5}\)
VẬY X=-3/4; Y=1/5; Z=11/20
B) \(|3x-4|+\left|3y-5\right|=0\)
\(\Rightarrow\left|3x-4\right|=\left|3y-5\right|=0\)
\(\Rightarrow\left|3x-4\right|=0\) \(\Rightarrow\left|3y-5\right|=0\)
\(3x-4=0\) \(3y-5=0\)
\(3x=4\) \(3y=5\)
\(x=\frac{4}{3}\) \(y=\frac{5}{3}\)
VẬY X= 4/3; Y=5/3
C) \(\left|x+\frac{3}{4}\right|+\left|y-\frac{2}{5}\right|+\left|z+\frac{1}{2}\right|< 0\)
ĐỂ \(\left|x+\frac{3}{4}\right|+\left|y-\frac{2}{5}\right|+\left|z+\frac{1}{2}\right|< 0\)
\(\Rightarrow\left|x+\frac{3}{4}\right|;\left|y-\frac{2}{5}\right|;\left|z+\frac{1}{2}\right|< 0\)
MÀ GIÁ TRỊ TUYỆT ĐỐI LUÔN MANG SỐ NGUYÊN DƯƠNG
\(\Rightarrow x;y;z\in\varnothing\)
d) \(\left|x+\frac{1}{5}\right|+\left|3-y\right|=0\)
\(\Rightarrow\left|x+\frac{1}{5}\right|=\left|3-y\right|=0\)
\(\Rightarrow\left|x+\frac{1}{5}\right|=0\) \(\Rightarrow\left|3-y\right|=0\)
\(x+\frac{1}{5}=0\) \(3-y=0\)
\(x=\frac{-1}{5}\) \(y=3\)
VẬY X= -1/5; Y=3
CHÚC BN HỌC TỐT!!!!!!!
Ta có :
\(\left|x+\frac{3}{4}\right|+\left|y-\frac{1}{5}\right|+\left|x+y+z\right|=0\)
\(\Leftrightarrow\)\(\hept{\begin{cases}x+\frac{3}{4}=0\\y-\frac{1}{5}=0\\x+y+z=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{-3}{4}\\y=\frac{1}{5}\\z=0-\frac{-3}{4}-\frac{1}{5}\end{cases}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}x=\frac{-3}{4}\\y=\frac{1}{5}\\z=\frac{11}{20}\end{cases}}\)
Vậy \(x=\frac{-3}{4};y=\frac{1}{5};z=\frac{11}{20}\)
\(b)\) Ta có :
\(\left|3x-4\right|+\left|3y-5\right|=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}3x-4=0\\3y-5=0\end{cases}\Leftrightarrow\orbr{\begin{cases}3x=4\\3y=5\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=\frac{4}{3}\\y=\frac{5}{3}\end{cases}}}\)
Vậy \(x=\frac{4}{3}\) và \(y=\frac{5}{3}\)
Tìm x,y,z thuộc Q:
a)|x+9/2|+|y+4/3|+|z+7/2| nhỏ hơn hoặc bằng 0
b)|x+3/4|+|y-2/5|+|z+1/2| nhỏ hơn hoặc bằng 0
c) |x+19/5|+|y+1890/1975|+|z-2004|=0
d) |x+3/4|+|y-1/5|+|x+y+z|=0
Giúp mk với mn ơi
a,Cho a2+b2+(a+b)2=c2+d2+(c+d)2. CM: a4+b4+(a+b)4=c4+d4+(c+d)4
b, Cho x,y,z là các số thực thỏa mãn: (x-y)2 + (y-z)2 + (z-x)2 = (x+y-2z)2 + (y+z-2x)2 + (x+z-2y)2. CM: x=y=z
c, Cho x, y là các số thỏa mãn: 2x2 +y3 - 4x + 3 = 0 và x2y2 + y2 - 2x=0. Tính giá trị biểu thức A= x100y1001 + x700y2
d, Cho x, y, z thỏa mãn (x+y+z)3 - x3 -y3 -z3 = 0. Tính giá trị biểu thức: P = (x2015 + y2015 )(y2017+ z2017)(z2019+x2019)
Tìm x,y thuộc Z:
a, (x-3)^2+(y+2)^2=0
b,2x+2^x+3=136
c,42-3./y-3/=4.(2042-x)^4
d,/x+5/+(3y-6)^2010=0
e,(2x-4)^2008+(y-4)^2008+/x+y+z/=0
g,(3x-6)^2006+(y^2-1)^2008+(x-z)^2100=0
h,8.2^3x.7^y=56^2x.5^x-1
i, x^3-y^3-z^3=3xyz và x^2=2.(y+z) (x,y,z thuộc N*)
Tìm x,y,z
a, | x - 1 | + | 2x - 5 | = 0
b, | x + 1/5 | + | 3 - y | = 0
c, | x + 3/4 | + | y - 2/5 | + | z + 1/2 | = 0
d, | x + 3/4 | + | y - 1/5 | + | x + y + z | = 0
giúp mk với nha các bn
trả lời ngay cho mình nhé
bài 1 tìm x thuộc Z
a) x^2+2.x=0
b) (-2.x).(-4.x)+28=100
c) 5.x.(-x)^2+1=6
d) 3.x^2+12.x=0
e) 4.x.3=4.x
bài 2: tìm x,y thuộc Z
a) (x+2).(x-1)=0
b) (y+1).(x.y-1)=3
c) 2.x.y+x-6.y=15
d) x.y+2.x-y+9
e)3.x.y-y=-12
g) 3.x.y-3.x-y=0
h) 5.x.y+5.x+2.y =-16
Bài 1:
a, \(x^2\) +2\(x\) = 0
\(x.\left(x+2\right)\) = 0
\(\left[{}\begin{matrix}x=0\\x+2=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
\(x\) \(\in\) {-2; 0}
b, (-2.\(x\)).(-4\(x\)) + 28 = 100
8\(x^2\) + 28 = 100
8\(x^2\) = 100 - 28
8\(x^2\) = 72
\(x^2\) = 72 : 8
\(x^2\) = 9
\(x^2\) = 32
|\(x\)| = 3
\(\left[{}\begin{matrix}x=-3\\x=3\end{matrix}\right.\)
Vậy \(\in\) {-3; 3}
c, 5.\(x\) (-\(x^2\)) + 1 = 6
- 5.\(x^3\) + 1 = 6
5\(x^3\) = 1 - 6
5\(x^3\) = - 5
\(x^3\) = -1
\(x\) = - 1
d, 3\(x^2\) + 12\(x\) = 0
3\(x.\left(x+4\right)\) = 0
\(\left[{}\begin{matrix}x=0\\x+4=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-4; 0}
e, 4.\(x.3\) = 4.\(x\)
12\(x\) - 4\(x\) = 0
8\(x\) = 0
\(x\) = 0
Cho x y z là các số thực khác 0 thỏa mãn x + y + z = 3 và x^2 + y^2 + z^2 = 9 . Tính GTBT : D = ( yz/x^2 + xz/y^2 + xy/z^2 -4)^2019
Tìm x,y,z thuộc Q:
a)|x+9/2|+|y+4/3|+|z+7/2| nhỏ hơn hoặc bằng 0
b)|x+3/4|+|y-2/5|+|z+1/2| nhỏ hơn hoặc bằng 0
c) |x+19/5|+|y+1890/1975|+|z-2004|=0
d) |x+3/4|+|y-1/5|+|x+y+z|=0
giúp mk nha mn mk đang cần gấp lắm
Hơi tắt nhá
a) Đặt \(\left|x+\dfrac{9}{2}\right|+\left|y+\dfrac{4}{3}\right|+\left|z+\dfrac{7}{2}\right|=A\)
\(\left|x+\dfrac{9}{2}\right|+\left|y+\dfrac{4}{3}\right|+\left|z+\dfrac{7}{2}\right|\ge0\forall x;y;z\)
mà A\(\le0\)
\(\left|x+\dfrac{9}{2}\right|+\left|y+\dfrac{4}{3}\right|+\left|z+\dfrac{7}{2}\right|\) phải bằng 0 đê thỏa mãn điều kiện
\(\Rightarrow\left\{{}\begin{matrix}\left|x+\dfrac{9}{2}\right|=0\\\left|y+\dfrac{4}{3}\right|=0\\\left|z+\dfrac{7}{2}\right|=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{9}{2}\\y=-\dfrac{4}{3}\\z=-\dfrac{7}{2}\end{matrix}\right.\)
Vậy....
b;c)I hệt câu a nên làm tương tự nhá
d)
Hơi tắt nhá
a) Đặt \(\left|x+\dfrac{3}{4}\right|+\left|y-\dfrac{1}{5}\right|+\left|x+y+z\right|=B\)
B=\(\left|x+\dfrac{3}{4}\right|+\left|y-\dfrac{1}{5}\right|+\left|x+y+z\right|=0\)
\(\Rightarrow\left\{{}\begin{matrix}\left|x+\dfrac{3}{4}\right|=0\\\left|y-\dfrac{1}{5}\right|=0\\\left|x+y+z\right|=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{3}{4}\\y=\dfrac{1}{5}\\x+y+z=0\end{matrix}\right.\)
Thay ra ta tính đc :\(z=-\dfrac{11}{20}\)
Vậy....
\(\left|x+\dfrac{9}{2}\right|+\left|y+\dfrac{4}{3}\right|+\left|z+\dfrac{7}{2}\right|\le0\)
\(\left\{{}\begin{matrix}\left|x+\dfrac{9}{2}\right|\ge0\\\left|y+\dfrac{4}{3}\right|\ge0\\\left|z+\dfrac{7}{2}\right|\ge0\end{matrix}\right.\)
\(\Rightarrow\left|x+\dfrac{9}{2}\right|+\left|y+\dfrac{4}{3}\right|+\left|z+\dfrac{7}{2}\right|\ge0\)
\(\Rightarrow\left[{}\begin{matrix}\left|x+\dfrac{9}{2}\right|+\left|y+\dfrac{4}{3}\right|+\left|z+\dfrac{7}{2}\right|\ge0\\\left|x+\dfrac{9}{2}\right|+\left|y+\dfrac{4}{3}\right|+\left|z+\dfrac{7}{2}\right|\le0\end{matrix}\right.\)
\(\Rightarrow\left|x+\dfrac{9}{2}\right|+\left|y+\dfrac{4}{3}\right|+\left|z+\dfrac{7}{2}\right|=0\)
\(\Rightarrow\left\{{}\begin{matrix}\left|x+\dfrac{9}{2}\right|=0\Rightarrow x=-\dfrac{9}{2}\\\left|y+\dfrac{4}{3}\right|=0\Rightarrow y=-\dfrac{4}{3}\\\left|z+\dfrac{7}{2}\right|=0\Rightarrow z=-\dfrac{7}{2}\end{matrix}\right.\)
\(\left|x+\dfrac{3}{4}\right|+\left|y-\dfrac{2}{5}\right|+\left|z+\dfrac{1}{2}\right|\le0\)
\(\left\{{}\begin{matrix}\left|x+\dfrac{3}{4}\right|\ge0\\\left|y-\dfrac{2}{5}\right|\ge0\\\left|z+\dfrac{1}{2}\right|\ge0\end{matrix}\right.\)
\(\Rightarrow\left|x+\dfrac{3}{4}\right|+\left|y-\dfrac{2}{5}\right|+\left|z+\dfrac{1}{2}\right|\ge0\)
\(\Rightarrow\left[{}\begin{matrix}\left|x+\dfrac{3}{4}\right|+\left|y-\dfrac{2}{5}\right|+\left|z+\dfrac{1}{2}\right|\ge0\\\left|x+\dfrac{3}{4}\right|+\left|y-\dfrac{2}{5}\right|+\left|z+\dfrac{1}{2}\right|\le0\end{matrix}\right.\)
\(\Rightarrow\left|x+\dfrac{3}{4}\right|+\left|y-\dfrac{2}{5}\right|+\left|z+\dfrac{1}{2}\right|=0\)
\(\Rightarrow\left\{{}\begin{matrix}\left|x+\dfrac{3}{4}\right|=0\Rightarrow x=-\dfrac{3}{4}\\\left|y-\dfrac{2}{5}\right|=0\Rightarrow y=\dfrac{2}{5}\\\left|z+\dfrac{1}{2}\right|=0\Rightarrow z=-\dfrac{1}{2}\end{matrix}\right.\)
\(\left|x+\dfrac{19}{5}\right|+\left|y+\dfrac{1890}{1975}\right|+\left|z-2004\right|=0\)
\(\left\{{}\begin{matrix}\left|x+\dfrac{19}{5}\right|\ge0\\ \left|y+\dfrac{1980}{1975}\right|\ge0\\\left|z-2004\right|\ge0\end{matrix}\right.\)
\(\left|x+\dfrac{19}{5}\right|+\left|y+\dfrac{1980}{1975}\right|+\left|z-2004\right|\ge0\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}\left|x+\dfrac{19}{5}\right|=0\Rightarrow x=-\dfrac{19}{5}\\ \left|y+\dfrac{1980}{1975}\right|=0\Rightarrow y=-\dfrac{1980}{1975}\\\left|z-2004\right|=0\Rightarrow z=2004\end{matrix}\right.\)
\(\left|x+\dfrac{3}{4}\right|+\left|y-\dfrac{1}{5}\right|+\left|x+y+z\right|=0\)
\(\left\{{}\begin{matrix}\left|x+\dfrac{3}{4}\right|\ge0\\ \left|y-\dfrac{1}{5}\right|\ge0\\\left|x+y+z\right|\ge0\end{matrix}\right.\)
\(\Rightarrow\left|x+\dfrac{3}{4}\right|+\left|y-\dfrac{1}{5}\right|+\left|x+y+z\right|\ge0\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}\left|x+\dfrac{3}{4}\right|=0\Rightarrow x=-\dfrac{3}{4}\\\left|y-\dfrac{1}{5}\right|=0\Rightarrow y=\dfrac{1}{5}\\\left|x+y+z\right|=0\Rightarrow z+-\dfrac{11}{20}=0\Rightarrow z=\dfrac{11}{20}\end{matrix}\right.\)
Đặt \(\left|x+\dfrac{9}{2}\right|+\left|y+\dfrac{4}{3}\right|+\left|z+\dfrac{7}{2}\right|=A\)
\(\Rightarrow A\ge0\)
Mà ĐK đề là \(A\le0\)
\(\Rightarrow A=0\)
\(\left[{}\begin{matrix}\left|x+\dfrac{3}{4}=0\right|\Rightarrow x=-\dfrac{3}{4}\\\left|y-\dfrac{2}{5}=0\right|\Rightarrow y=\dfrac{2}{5}\\\left|z+\dfrac{1}{2}=0\right|\Rightarrow z=-\dfrac{1}{2}\end{matrix}\right.\)
Các câu còn lại tương tự nhé
1.Tìm x, y, z, biết:
a,11x=8y;7y=11z va x+y-10z=-102
c, x/y=9/25; y/z=10/13 và x-3y+2z=6
2. Tìm x, y, z biết:
a, x/8= y/3 = z/10 và xy +yz+zx=1206
b, x/4=2y/5=5z/6 và x^2-3y^2+2z^2=325.
3. Cho b^2=ac, c^2=bd vs b,c,d khác 0 và b+c+d khác 0. CM: a^3+b^3+c^3/b^3+c^3+d^3=(a+b+c/b+c+d)^2
4. Cho a,b,c khác 0 thỏa mãn: b^2=ac. CMR: a/c=(a+2018b/b+2018c)^2
Giúp mk vs nha. Mk sẽ tick choa.