Số đỉnh của khối bát diện đều là:
A. 6
A. 6
C. 8
C. 8
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho hình bát diện đều ABCDEF cạnh a. Tính theo a thể tích V của khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện (xem hình vẽ)
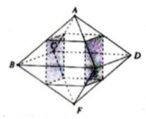
A. V = a 3 2 .
B. V = a 3 2 4 .
C. V = a 3 2 2 .
D. V = a 3 2 8 .
Phương pháp:
Khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện đều ABCDEF (như hình vẽ) là hình hộp chữ nhật.
Cách giải:
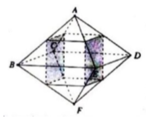
Khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện đều ABCDEF là hình hộp chữ nhật có đáy là hình vuông cạnh a 2 ;

Số đỉnh của khối bát diện đều là:
A. 6.
B. 7.
C. 8.
D. 9.
Số đỉnh của khối bát diện đều là:
A. 6
B. 7
C. 8
D. 9
Số đỉnh của một hình bát diện đều là:
A. Sáu B. Tám
C. Mười D. Mười hai.
Chọn A.
Làm tương tự bài 1.40: 2c = 3 x 8 = 4đ, suy ra đ = 6.
Hình lập phương là hình :
A. Có 6 mặt đều là hình vuông,có 8 đỉnh và 12 cạnh bằng nhau
B. Có 6 mặt đều là hình chữ nhật,có 8 đỉnh và 12 cạnh bằng nhau
C. Có 6 mặt đều là hình chữ nhật,có 12 đỉnh và 8 cạnh
A. Có 6 mặt đều là hình vuông,có 8 đỉnh và 12 cạnh bằng nhau
Tính thể tích của khối lập phương có các đỉnh là trọng tâm các mặt của khối bát diện đều cạnh a
A. V = 8 a 3 27
B. V = a 3 27
C. V = 16 a 3 2 27
D. V = 2 a 3 2 27
Đáp án D
Khối lập phương có các đỉnh lần lượt là trọng tâm các mặt của khối bát diện đều cạnh a có độ dài cạnh bằng x = 2 3 . a 2 2 = a 2 3 . Vậy thể tích cần tính là V = x 3 = 2 a 3 3 = 8 a 3 27
Tính thể tích của khối lập phương có các đỉnh là trọng tâm các mặt của khối bát diện đều cạnh a
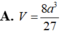
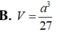
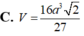
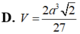
Thể tích V của khối lập phương có các đỉnh là trọng tâm các mặt của một khối bát diện đều cạnh a là
A. V = 8 a 3 27
B. V = a 3 27
C. V = 16 a 3 2 27
D. V = 2 a 3 2 27
Chọn D
Tính độ dài một cạnh của hình lập phương theo a bằng cách sử dụng định lý Ta-lét