Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Số đỉnh của một hình bát diện đều là:
A. Sáu B. Tám
C. Mười D. Mười hai.
Thể tích V của khối lập phương có các đỉnh là trọng tâm các mặt của một khối bát diện đều cạnh a là
Đọc tiếp
Thể tích V của khối lập phương có các đỉnh là trọng tâm các mặt của một khối bát diện đều cạnh a là
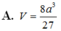
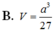
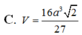
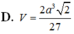
Đếm số đỉnh, số cạnh của khối bát diện đều.
Gọi M, C, Đ thứ tự là số mặt, số cạnh, số đỉnh của hình bát diện đều. Khi đó S=M+C+Đ bằng:
A. S=24
B. S=26
C. S=30
D. S=14
Cho tứ diện đều ABCD cạnh 2a. Tính thể tích của khối bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện ABCD.
Đọc tiếp
Cho tứ diện đều ABCD cạnh 2a. Tính thể tích của khối bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện ABCD.
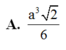
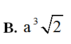
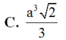
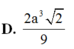
Kí hiệu M là số mặt, Đ là số đỉnh và C là số cạnh của một hình bát diện đều. Khi đó bộ (M, Đ, C) tương ứng với bộ số nào? A. (M, Đ, C)(6,12,8) B. (M, Đ, C)(8,12,6) C. (M, Đ, C)(8,6,12) D. (M, Đ, C)(12,8,6)
Đọc tiếp
Kí hiệu M là số mặt, Đ là số đỉnh và C là số cạnh của một hình bát diện đều. Khi đó bộ (M, Đ, C) tương ứng với bộ số nào?
A. (M, Đ, C)=(6,12,8)
B. (M, Đ, C)=(8,12,6)
C. (M, Đ, C)=(8,6,12)
D. (M, Đ, C)=(12,8,6)
Kí hiệu M là số mặt, Đ là số đỉnh và C là số cạnh của một hình bát diện đều. Khi đó bộ (M, Đ, C) tương ứng với bộ số nào? A. (M, Đ, C) (6,12,8) B. (M, Đ, C) (8,6,12) C. (M, Đ, C) (12,8,6) D. (M, Đ, C) (8,12,6)
Đọc tiếp
Kí hiệu M là số mặt, Đ là số đỉnh và C là số cạnh của một hình bát diện đều. Khi đó bộ (M, Đ, C) tương ứng với bộ số nào?
A. (M, Đ, C) = (6,12,8)
B. (M, Đ, C) = (8,6,12)
C. (M, Đ, C) = (12,8,6)
D. (M, Đ, C) = (8,12,6)
Thể tích V của khối lập phương có các đỉnh là trọng tâm các mặt của một khối bát diện đều cạnh bằng 1 là:
Đọc tiếp
Thể tích V của khối lập phương có các đỉnh là trọng tâm các mặt của một khối bát diện đều cạnh bằng 1 là:
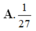
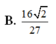
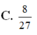
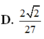
Số đỉnh của hình bát diện đều là:
A. 6
B. 8
C. 10.
D. 12.

