Cho hình phẳng (H)giới hạn bởi các đường y = sin x trục hoành và x=0; x = π . Thể tích vật thể tròn xoay sinh bởi hình (H) quay quanh trục Ox bằng

A..

B..

C..

D..

Cho hình phẳng (H) giới hạn bởi các đường y = xlnx , trục hoành, đường thẳng x = 1 2 . Tính diện tích hình phẳng (H).

A. 1 16 − 1 8 ln 2

B.  3 16 − 1 8 ln 2

C.  3 16 + 1 8 ln 2

D.  1 8 3 − ln 2

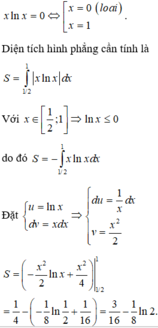
Cho hình phẳng H giới hạn bởi các đường y = x ln x , trục hoành, đường thẳng x = 1 2 . Tính diện tích hình phẳng  H .

A.  1 8 3 - ln 2

B. 3 16 - 1 8 ln 2

C. 3 16 + 1 8 ln 2

D. 1 16 - 1 8 ln 2

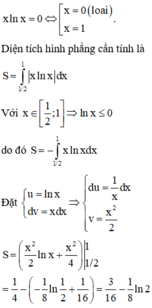
Cho hình phẳng (H) giới hạn bởi các đường y = x ln x , trục hoành, đường thẳng x = 1 2 . Tính diện tích hình phẳng (H).

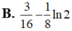
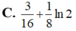
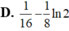
Cho hình phẳng (H) giới hạn bởi các đường x y = 4 ,   x = 0 ,   y = 1   v à   y = 4 . Tính thể tích V của khối tròn xoay tạo thành khi quay hình (H) quanh trục tung.

A.  V = 8 π

B. V = 10 π

C. V = 12 π

D. V = 16 π

Cho (H) là hình phẳng giới hạn bởi các đường y = - x , y = x , x = 4  . Tính thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Ox.

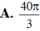
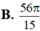
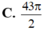
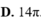
Cho hình phẳng giới hạn bởi đồ thị các hàm số  y = x , đường thẳng y = 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là

A.  7 6 .

B.  4 3 .

C.  5 6 .

D.  5 4 .

Cho hình phẳng (H) giới hạn bởi các đường y = x − 2 ln x + 1 , hai trục tọa độ. Diện tích S của hình phẳng (H) là

A.  S = 3 − 2 ln 3.

B.  S = 12 − 9 ln 3.

C.  S = 4 − 9 2 ln 3.

D.  S = 9 2 ln 3 − 4.