Trên tập hợp số phức, cho phương trình z 2 + bz + c = 0 với b,c ∈ ℚ Biết rằng hai nghiệm của phương trình có dạng w + 3 và 2w – 6i +1 với w là một số phức. Tính S = b 3 - c 2 .
A. S = -1841.
B. S = -3.
C. S = 7.
D. S = 2161.
Trên tập hợp số phức cho phương trình z 2 + b z + c = 0 với b , c ∈ R . Biết rằng hai nghiệm của phương trình có dạng w + 3 và 3 w − 8 i + 13 với w là số phức. Tính S = b 2 − c 3 .
A. S = -496.
B. S = 0.
C. S = -26.
D. S = 8.
Đáp án A.
Đặt
z 1 = w + 3 = m + n i ; z 2 = 3 w − 8 i + 13 = m − n i .
Ta có:
w = z 1 − 3 = z 2 + 8 i − 13 3 ⇒ m + n i − 3 = 1 3 m − n i + 8 i − 13 ⇔ 2 m + 4 + 4 n − 8 i = 0 ⇔ m = − 2 n = 2
Do đó:
− b = z 1 + z 2 = 2 m = − 4 c = z 1 z 2 = − 2 + 2 i − 2 − 2 i = 4 − 4 i 2 = 8 ⇒ b = 4 c = 8 .
Do đó b 2 − c 3 = 4 2 − 8 3 = − 496.
Trên tập số phức, cho phương trình a z 2 + b z + c = 0 (a,b,c∈R;a≠0). Chọn kết luận sai
A. Nếu b=0 thì phương trình có hai nghiệm mà tổng bằng 0
B. Nếu Δ = b 2 - 4 ac < 0 thì phương trình có hai nghiệm mà modun bằng nhau
C. Phương trình luôn có hai nghiệm phức là liên hợp của nhau
D. Phương trình luôn có nghiệm
Xét phương trình bậc hai az2+bz+c=0 trên tập C a ≠ 0 , a , b , c ∈ R . Tìm điều kiện cần và đủ để phương trình có hai nghiệm z1 và z2 là số phức liên hợp với nhau.
![]()
![]()
![]()
![]()
Cho số phức thỏa mãn z - i = z - 1 + 2 i . Tập hợp điểm biểu diễn số phức w = (2 - i) z +1 trên mặt phẳng phức là một đường thẳng. Phương trình của đường thẳng đó là
![]()
![]()
![]()
![]()
Trên tập số phức C, cho phương trình a z 2 + b z + c = 0 ( a , b , c ∈ R ; a ≠ 0 ). Khẳng định nào sau đây sai
A. Tổng hai nghiệm của phương trình bằng -b/a.
B. Δ = b 2 - 4 a c < 0 thì phương trình vô nghiệm.
C. Phương trình luôn có nghiệm.
D. Tích hai nghiệm của phương trình là c/a
Trên tập số phức C, cho phương trình a z 2 + b z + c = 0 a , b , c ∈ R , a ≠ 0 . Khẳng định nào sau đây sai?
A. Tổng hai nghiệm của phương trình bằng - b a .
B. △ = b 2 - 4 a c < 0 thì phương trình vô nghiệm
C. Phương trình luôn có nghiệm
D. Tích hai nghiệm của phương trình là b a
Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 = 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau?
1. Phương trình vô nghiệm trên trường số thực R.
2. Phương trình vô nghiệm trên trường số phức C
3. Phương trình không có nghiệm thuộc tập số thực.
4. Phương trình có bốn nghiệm thuộc tập số phức.
5. Phương trình chỉ có hai nghiệm là số phức.
6. Phương trình có hai nghiệm là số thực
A. 0.
B. 1.
C. 3.
D. 2.
Chọn D.
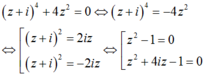
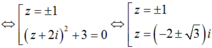
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.
Trên mặt phẳng phức tập hợp các số phức z = x + yi thỏa mãn |z + 2 - i| = | z ¯ - 3i| là đường thẳng có phương trình
A. y = x + 1
B. y = -x + 1
C. y = -x - 1
D. y = x - 1
Cho số phức z có tập hợp điểm biểu diễn trên mặt phẳng phức là đường tròn có phương trình x 2 + y 2 - 25 = 0 . Tính môđun của số phức z?
![]()
![]()
![]()
![]()