Gọi S là tập tất cả các giá trị nguyên không dương của m để phương trình log 1 3 x + m + log 3 3 - x = 0 có tập nghiệm. Tập S có bao nhiêu tập con?
A. 4
B. 8
C.. 2
D. 7
Cho hệ phương trình 2 x − y − 2 y + x = 2 y 2 x + 1 = m + 2 2 .2 y . 1 − y 2 ( 1 ) , m là tham số. Gọi S là tập các giá trị nguyên để hệ (1) có một nghiệm duy nhất. Tập S có bao nhiêu phần tử?
A. 0
B. 1
C. 3
D. 2
Chọn B.
Phương pháp:
+ Biến đổi phương trình thứ nhất của hệ để đưa về dạng
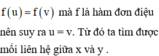
+ Thay vào phương trình thứ hai ta được phương trình ẩn y. Lập luận phương trình này có nghiệm duy nhất
thì hệ ban đầu sẽ có nghiệm duy nhất.
+ Sử dụng bất đẳng thức Cô-si để thử lại m.
Cách giải:
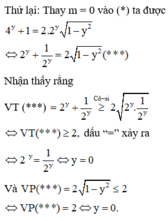
Vậy phương trình (***) có nghiệm duy nhất y = 0.
Kết luận : Với m = 0 thì hệ đã cho có nghiệm duy nhất nên tập S có một phần tử.
Chú ý :
Các em có thể làm bước thử lại như sau :
Thay m = 0 vào (*) ta được
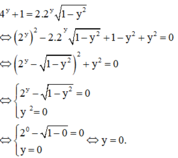
Cho S là tập hợp các giá trị thực của tham số m để phương trình 2 − x + 1 − x = m + x − x 2 có hai nghiệm phân biệt. Tổng các số nguyên trong S bằng
A. 11
B. 0
C. 5
D. 6
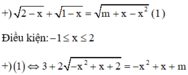
Đặt − x 2 + x = t ;
f x = − x 2 + x ; f ' x = − 2 x + 1
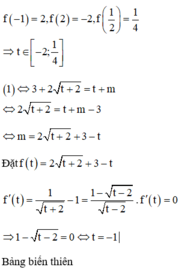
Chọn A
Cho S là tập hợp các giá trị thực của tham số m để phương trình 2 - x + 1 - x = m + x - x 2 có hai nghiệm phân biệt. Tổng các số nguyên trong S bằng
A. 11.
B. 0.
C. 5.
D. 6.
Đáp án A
+)
(
)
Điều kiện:
+)
Đặt:
Đặt
.
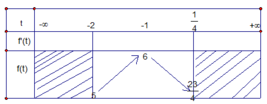
Bảng biến thiên
+) 
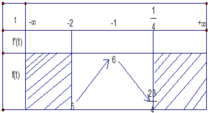
Để phương trình có hai nghiệm phân biệt
Do đó để phương trình có hai nghiệm phân biệt thì phương trình
có nghiệm
Từ bảng biến thiên
.
Cho phương trình 4 6 + x - x 2 - 3 x = m x + 2 + 2 3 - x với m là tham số. Hỏi có bao nhiêu giá trị nguyên của m để phương trình có nghiệm?
A. 10
B. 9
C. 11
D. 8
Chọn đáp án A
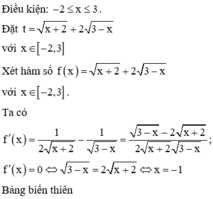
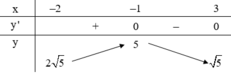
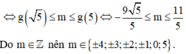
Vậy số giá trị nguyên của m để phương trình có nghiệm là 10.
Gọi S là tập hợp các giá trị thực của tham số m để phương trình 4 x - m . 2 x + 2 m + 1 = 0 có nghiệm. Tập R\S có bao nhiêu giá trị nguyên?
A.1
B.4
C.9
D.7
Gọi S là tập hợp các giá trị thực của tham số m để phương trình 4 x – m . 2 x + 2 m + 1 = 0 có nghiệm. Tập R\S có bao nhiêu giá trị nguyên
A. 1
B. 4
C. 9
D. 7
Cho phương trình:
sin 3 x + 2 sin x + 3 = 2 c o s 3 x + m 2 c o s 3 x + m - 2 + 2 c o s 3 x + c o s 2 x + m .
Có bao nhiêu giá trị nguyên của tham số m để phương trình trên có đúng 1 nghiệm x ∈ 0 ; 2 π 3 ?
A. 2
B. 1
C. 3
D. 4
Cho phương trình
\(\left(m-1\right)x^2-2\left(m-3\right)x+m+1\)1=0
Với điều kiện của m để phương trình có 2 nghiệm x1, x2, gọi S và P lần lượt là tổng và tích của 2 nghiệm của phương trình. Tìm các giá trị của m để S và P là các số nguyên
Có bao nhiêu giá trị nguyên của tham số m để phương trình x^2 -2|x| +1-m = 0 có 4 nghiệm phân biệt ?
Đặt \(\left|x\right|=t\ge0\)
\(\Rightarrow t^2-2t+1-m=0\) (1)
Phương trình (1) là bậc 2 nên có đối đa 2 nghiệm t
Với mỗi giá trị \(t>0\) cho 2 nghiệm x tương ứng nên pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=1-\left(1-m\right)>0\\t_1+t_2=2>0\\t_1t_2=1-m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\m< 1\end{matrix}\right.\) \(\Leftrightarrow0< m< 1\)
