Tìm các số thực x và y thỏa mãn điều kiện (2x+1)+(3y-2)i(x+2)+(y+4)i A. . B. . C. . D..
Đọc tiếp
Tìm các số thực x và y thỏa mãn điều kiện (2x+1)+(3y-2)i=(x+2)+(y+4)i
A. 
.
B. 
.
C. 
.
D.
.
PB
Những câu hỏi liên quan
Tìm các số thực x, y thỏa mãn:
a) 2x + 1 + (1 – 2y)i = 2 – x + (3y – 2)i
b) 4x + 3 + (3y – 2)i = y +1 + (x – 3)i
c) x + 2y + (2x – y)i = 2x + y + (x + 2y)i
a)tìm các cặp số nguyên dương x,y thỏa mãn: 2x^2+3y^2-5xy-x+3y-4=0
b) các số x,y,z thỏa mãn điều kiện x^2+y^2+z^2=2014. tìm giá trị nhỏ nhất của M=2xy-yz-xz
Tìm các số thực x,y thỏa mãn
2
x
-
1
+
(
1
-
2
y
)
i
2
-
x
+
(
3
y
+
2
)
i
A.
x
1
;
y
3
5
B.
x
3
;
y
3...
Đọc tiếp
Tìm các số thực x,y thỏa mãn 2 x - 1 + ( 1 - 2 y ) i = 2 - x + ( 3 y + 2 ) i
A. x = 1 ; y = 3 5
B. x = 3 ; y = 3 5
C. x = 3 ; y = - 1 5
D. x = 1 ; y = - 1 5
Tìm các số thực x, y thỏa mãn: 2x + 1 + (1 – 2y)i = 2 – x + (3y – 2)i
Tìm các số thực x,y,z thỏa mãn đồng thời các điều kiện x-1/2=y+1/3=t-3/5 và 2x+y-z
Tìm các số thực x,y,z thỏa mãn dồng thời các điều kiện x-1/2=y+1/3=z-3/5 và 2x+y-z=0
Ta có: \(\dfrac{x-1}{2}=\dfrac{y+1}{3}=\dfrac{z-3}{5}\)
nên \(\dfrac{2x-2}{4}=\dfrac{y+1}{3}=\dfrac{z-3}{5}\)
mà 2x+y-z=0
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x-2}{4}=\dfrac{y+1}{3}=\dfrac{z-3}{5}=\dfrac{2x+y-z-2+1+3}{4+3-5}=\dfrac{2}{2}=1\)
Do đó: x=3; y=2; z=8
Đúng 1
Bình luận (0)
Tìm các số thực \(x,y\) thỏa mãn :
a) \(2x+1+\left(1-2y\right)i=2-x+\left(3y-2\right)i\)
b) \(4x+3+\left(3y-2\right)i=y+1+\left(x-3\right)i\)
c) \(x+2y+\left(2x-y\right)i=2x+y+\left(x+2y\right)i\)
Cho x, y, z là các số thực thỏa mãn điều kiện
4
x
+
9
y
+
16
z
2
x
+
3
y
+
4
z
. Tìm giá trị lớn nhất của biểu thức
T
2
x
+
1
+...
Đọc tiếp
Cho x, y, z là các số thực thỏa mãn điều kiện 4 x + 9 y + 16 z = 2 x + 3 y + 4 z . Tìm giá trị lớn nhất của biểu thức T = 2 x + 1 + 3 y + 1 + 4 z + 1
A. 13 + 87 2
B. 11 + 87 2
C. 7 + 37 2
D. 9 + 87 2
Cho x, y, z là các số thực thỏa mãn điều kiện
4
x
+
9
y
+
16
z
2
x
+
3
y
+
4
z
. Tìm giá trị lớn nhất của biểu thức
T
...
Đọc tiếp
Cho x, y, z là các số thực thỏa mãn điều kiện 4 x + 9 y + 16 z = 2 x + 3 y + 4 z . Tìm giá trị lớn nhất của biểu thức T = 2 x + 1 + 3 y + 1 + 4 z + 1
Các số thực x, y thỏa mãn:
(
2
x
+
3
y
+
1
)
+
(
-
x
+
2
y
)
i
(
3
x
-
2
y
+
2
)
+
(
4...
Đọc tiếp
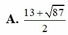
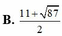
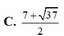
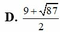
Các số thực x, y thỏa mãn: ( 2 x + 3 y + 1 ) + ( - x + 2 y ) i = ( 3 x - 2 y + 2 ) + ( 4 x - y - 3 ) i là
A. x ; y = - 9 11 ; - 4 11
B. x ; y = 9 11 ; 4 11
C. x ; y = 9 11 ; - 4 11
D. x ; y = - 9 11 ; 4 11
