Phương trình mặt phẳng Oxyz chứa trục Oz và cắt mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 x + 2 y - 6 = 0 theo đường tròn có bán kính bằng 3 là
A. x+y=0
B. x-y=0
C. x+2y=0
D. x-2y=0
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và mặt cầu (S): x²+y²+z²+2x-6y+4z-15=0. Mặt phẳng chứa d, tiếp xúc với (S) và cắt trục Oz tại điểm có cao độ lớn hơn 3 có phương trình là:
A. 2x-3y+4z-10=0.
B. 2x-3y+4z-12=0.
C. 3x-4y+2z-12=0.
D. 3x-4y+2z-10=0.
Chọn D
Mặt cầu (S) có tâm I (-1;3;-2) và bán kính R = √29.
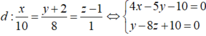
Mặt phẳng (P) chứa d có dạng m (4x-5y-10)+n (y-8z+10)=0
ó 4mx + (n – 5m)y – 8nz + 10n – 10m = 0 với m²+n²>0.
(P) tiếp xúc với (S) nên d (I, (P)) = R
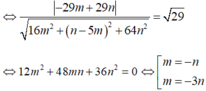
Trường hợp 1: m = -n, phương trình mặt phẳng (P): 2x-3y+4z-10=0.
Khi đó giao điểm của (P) và Ox có tọa độ là (0;0;5/2) (nhận)
Trường hợp 2: m = -3n, phương trình mặt phẳng (P):x-2y+6z-10=0.
Khi đó giao điểm của (P) và Ox có tọa độ là (0;0;5/3) (loại).
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là: ( x + 1 ) 2 + ( y - 4 ) 2 + ( z + 3 ) 2 = 36. Số mặt phẳng (P) chứa trục Ox và tiếp xúc với mặt cầu (S) là:
A. 0
B. 1
C. 2
D. Vô số
Đáp án A
Mặt cầu (S) có tâm I(-1;4;-3) và có bán kính R = 6. Gọi H là hình chiếu vuông góc của I trên trục Ox. Ta có H(-1;0;0) và IH=5.
Gọi K là hình chiếu vuông góc của I trên mặt phẳng (P). Ta có
d(I; (P)) = IK ≤ IH = 5 < R = 6
Do đó mặt phẳng (P) luôn cắt mặt cầu (S) theo một đường tròn. Vậy không tồn tại mặt phẳng (P) chứa Ox và tiếp xúc với (S)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình x − 1 2 + y − 2 2 + z + 1 2 = 1 , phương trình mặt phẳng (Q) chứa trục hoành và tiếp xúc với mặt cầu (S) là
A. Q : 4 y + 3 z = 0
B. Q : 4 y + 3 z + 1 = 0
C. Q : 4 y − 3 z + 1 = 0
D. Q : 4 y − 3 z = 0
Đáp án là A.
+ Mặt phẳng chứa Ox có dạng B y + C z = 0
+ Do mặt cầu tiếp xúc với mặt phẳng nên:
2 B − C B 2 + C 2 = 1 ⇔ B = 0 B = 4 , C = 3
Vậy mặt phẳng cần tìm 4 y + 3 z = 0
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình x - 1 2 + y - 2 2 + z + 1 2 = 1 , phương trình mặt phẳng (Q) chứa trục hoành và tiếp xúc với mặt cầu (S) là
A. (Q): 4y +3z = 0
B. (Q): 4y +3z +1= 0
C. (Q): 4y -3z +1= 0
D. (Q): 4y -3z = 0
Đáp án là A.
+ Mặt phẳng chứa Ox có dạng By+Cz=0
+ Do mặt cầu tiếp xúc với mặt phẳng nên 2 B - C B 2 + C 2 = 1 ⇔ B = 0 B = 4 , C = 3
Vậy mặt phẳng cần tìm 4y +3z=0
Trong không gian Oxyz cho mặt cầu (S): x 2 + y 2 + z 2 − 2 x + 4 y − 16 = 0 và hai đường thẳng Δ 1 : x − 1 2 = y + 4 − 3 = z 2 và Δ 2 : x + 1 1 = y − 2 1 = z − 1 − 1 .Viết phương trình mặt phẳng α song song với Δ 1 , Δ 2 , tiếp xúc với mặt cầu (S) và cắt trục Oz tại điểm có cao độ dương
A. x − 4 y + 5 z − 7 − 21 2 = 0
B. x − 4 y + 5 z + 7 − 21 2 = 0
C. x + 4 y + 5 z − 7 − 21 2 = 0
D. x + 4 y + 5 z + 7 − 21 2 = 0
Trong không gian Oxyz cho mặt cầu (S): x 2 + y 2 + z 2 − 2 x + 4 y − 16 = 0 và hai đường thẳng Δ 1 : x − 1 2 = y + 4 − 3 = z 2 và Δ 2 : x + 1 1 = y − 2 1 = z − 1 − 1 .Viết phương trình mặt phẳng α song song với Δ 1 , Δ 2 , tiếp xúc với mặt cầu (S) và cắt trục Oz tại điểm có cao độ dương.
A. x − 4 y + 5 z − 7 − 21 2 = 0
B. x − 4 y + 5 z + 7 − 21 2 = 0
C. x + 4 y + 5 z − 7 − 21 2 = 0
D. x + 4 y + 5 z + 7 − 21 2 = 0
Đáp án D
Mặt cầu (S) có tâm I 1 ; − 2 ; 0 và bán kính R = 21
Đường thẳng Δ 1 có vtcp u 1 → = 2 ; − 3 ; 2 và đường thẳng Δ 2 có vtcp u 2 → = 1 ; 1 ; − 1
Mặt phẳng α có vtcp n → = u 1 → , u 2 → = 1 ; 4 ; 5 ⇒ α : x + 4 y + 5 z + m = 0
Do tiếp xúc với mặt cầu (S) nên
d I , α = 21 ⇔ 1 + 4. − 2 + 5.0 + m 1 2 + 4 2 + 5 2 = 21 ⇔ m = 7 + 21 2 m = 7 − 21 2
Do α cắt trục Oz tại điểm có cao độ dương ta có phương trình của α : x + 4 y + 5 z + 7 − 21 2 = 0
Trong không gian với hệ tọa độ Oxyz cho mặt cầu (S) có phương trình x - 1 2 + y - 2 2 + z + 1 2 = 1 . Một phương trình mặt phẳng (Q) chứa trục hoành và tiếp xúc với mặt cầu (S) là:
A. 4y + 3z = 0
B. 4y + 3z + 1 = 0
C. 4y - 3z + 1 = 0
D. 4y - 3z = 0
Chọn A
Mặt cầu (S) có tâm I (1; 2; -1) và bán kính R = 1
Gọi vectơ pháp tuyến của mặt phẳng (Q) là ![]() với
với
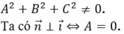
Mặt khác (Q) chứa trục hoành nên (Q) có phương trình dạng (Q): By + Cz = 0
Lại có (Q) tiếp xúc mặt cầu (S) nên
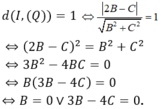
+ Với B = 0 thì phương trình mặt cầu là z = 0 ( chính là mặt phẳng 0xy)
+ Với 3B – 4C = 0, chọn B = 4 => C = 3. Vậy (Q): 4y + 3z = 0
Trong không gian Oxyz cho mặt cầu (S) x 2 + y 2 + z 2 - 2 x - 4 y - 6 z - 2 = 0 và mặt phẳng α 4 x + 3 y - 12 z + 10 = 0 . Lập phương trình mặt phẳng β thỏa mãn đồng thời các điều kiện: Tiếp xúc với (S), song song với α và cắt trục Oz ở điểm có cao độ dương
A. 4 x + 3 y - 12 z - 78 = 0
B. 4 x + 3 y - 12 z - 26 = 0
C. 4 x + 3 y - 12 z + 78 = 0
D. 4 x + 3 y - 12 z + 26 = 0
Ta có:
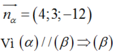
nhận n α → 4 ; 3 ; - 12 làm VTPT.
![]()
Ta có: (S) có tâm I 1 ; 2 ; 3 và bán kính
![]()
Mặt phẳng β tiếp xúc với mặt cầu
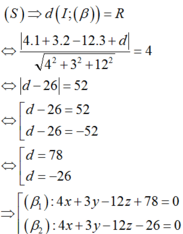
Gọi M 0 ; 0 ; z 0 z 0 > 0 là giao điểm của Oz và các mặt phẳng β 1 ; β 2
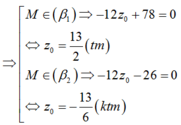
Chọn C.
Trong không gian Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 6 x + 4 y - 2 z + 5 = 0 Phương trình mặt phẳng (Q) chứa trục Ox và cắt (S) theo giao tuyến là một đường tròn bán kính bằng 2 là
A. (Q): 2y+z=0
B. (Q): 2x-z=0
C. (Q): y-2z=0
D. (Q): 2y-z=0
Đáp án D
Phương pháp:
![]()
Trong đó
d: khoảng cách từ tâm O đến mặt phẳng (P),
r: bán kính đường tròn là giao tuyến của mặt cầu (S) và mặt phẳng (P)
R: bán kính hình cầu.
Cách giải:
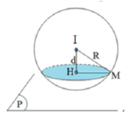
( S ) : x 2 + y 2 + z 2 - 6 x + 4 y - 2 z + 5 = 0
![]()
=> (S) có tâm I(3;-2;1) bán kính R = 3
(Q) cắt (S) theo giao tuyến là một đường tròn bán kính r = 2
Ta có
![]()
![]()
là một VTCP (Q)
Khi đó
![]()
![]()
![]()
Phương trình mặt phẳng (Q) đi qua O(0;0;0) và có VTPT n → =(0;b;c) là:
![]()
![]()
Khoảng cách từ tâm I đến (Q):
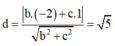
![]()
![]()
![]()
![]()
Phương trình mặt phẳng (Q): 2y -z =0