Cho hình chóp đều S.ABC có AB = a, A S B ^ = 30 ° . Lấy các điểm B', C' lần lượt thuộc các cạnh SB, SC sao cho chu vi tam giác AB'C' nhỏ nhất. Tính chu vi đó.
A. ( 3 -1)a
B. 3 a
C. a 3 + 1
D. (1+ 3 )a
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho hình chopstam giác đều S.ABC có cạnh AB = a . Các cạnh bên SA, SB, SC tạo với đáy một góc 60độ .Gọi D là giao điể chm của SA với mặt phẳng qua BC và vuông góc với SA
a) Tính tỉ số thể tích của 2 khối chóp S.DBC và S.ABC
b) Tính thể tích khối chóp S.DBC
Cho hình chóp đều S.ABC có A B = a , A S B ^ = 30 0 . Lấy các điểm B',C' lần lượt thuộc các cạnh SB, SC sao cho chu vi tam giác AB'C' nhỏ nhất. Tính chu vi đó
A. 3 - 1 a .
B. 3 a .
C. a 1 + 3 .
D. 1 + 3 a .
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a Các mặt bên (SAB),(SAC),(SBC) lần lượt tạo với đáy các góc lần lượt 30 độ, 45 độ, 60 độ Tính thể tích V của khối chóp S.ABC biết rằng hình chiếu vuông góc của S trên mặt phẳng (ABC) nằm bên trong tam giác ABC.
A. V = a 3 3 4 + 3
B. V = a 3 3 2 4 + 3
C. V = a 3 3 4 4 + 3
D. V = a 3 3 8 4 + 3
Cho hình chóp S.ABC có đáy là tam giác vuông tại A, A B C ^ = 30 0 , SAB là tam giác đều cạnh a, hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm của cạnh AB. Thể tích của khối chóp S.ABC là:
A. a 3 3 9
B. a 3 18
C. a 3 3 3
D. a 3 12
Một hình chóp tam giác đều S.ABC có AB=a cạnh bên SA tạo với đáy một góc 30 ° . Một hình nón có đỉnh S, đáy là hình tròn ngoại tiếp tam giác ABC. Tính số đo góc ở đỉnh α của hình nón đã cho
A. 120 °
B. 60 °
C. 150 °
D. 30 °
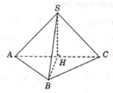
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, đỉnh S cách đều các điểm A,B,C. Biết AC = 2a,BC = a; góc giữa đường thẳng SB và mặt đáy (ABC) bằng 60 o . Tính theo a thể tích V của khối chóp S.ABC?
A. V = a 6 3 4 .
B. V = a 6 3 6 .
C. V = a 3 2 .
D. V = a 6 3 12 .
Đáp án C.
Hướng dẫn giải: Gọi H là trung điểm AC.
Do tam giác ABC vuông tại B nên H là tâm đường tròn ngoại tiếp tam giác ABC.
Đỉnh S cách đều các điểm A, B,C nên hình chiếu của S trên mặt đáy (ABC) trùng với tâm đường tròn ngoại tiếp tam giác ABC
suy ra S H ⊥ ( A B C )
![]()
Tam giác vuông SBH, có
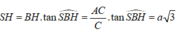
Tam giác vuông ABC ,
có A B = A C 2 - B C 2 = a 3
Diện tích tam giác vuông
S ∆ A B C = 1 2 B A . B C = a 3 2 2
Vậy V S . A B C = 1 3 S ∆ A B C . S H = a 3 2
Cho hình chóp đều S.ABC có AB=2a, khoảng cách từ A đến mp(SBC) là 3 a 2 . Tính thể tích hình chóp S.ABC
A. 3 a 3
B. 3 a 3 2
C. 3 a 3 6
D. 3 a 3 3
Đáp án là D
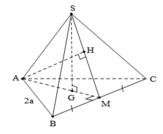
Gọi M là trung điểm của BC và G là tâm đường tròn ngoại tiếp tam giác ABC
Do S.ABC là hình chóp đều nên SG ⊥ (ABC) và G là trọng tâm tam giác ABC
Ta có:
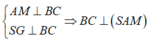
hay (SBC) ⊥ (SAM) theo giao tuyến SM
Trong (SAM) kẻ
![]()
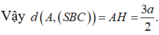
Vì tam giác ABC là tam giác đều cạnh 2a nên
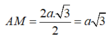
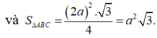
Đặt SG=x Ta có:
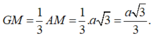
Xét tam giác SGM vuông tại M ta có:
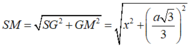
Xét tam giác SAM ta có
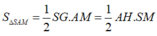
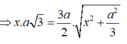
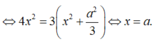
Do đó: SG=a.
Thể tích khối chóp S.ABC là
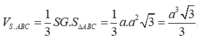
Cho hình chóp S.ABC có SA ⊥ (ABC), đáy ABC là tam giác đều. Tính thể tích khối chóp S.ABC biết AB = a; SA = a.
A. a 3 3 12
B. a 3 3 4
C. a 3
D. a 3 3
Chọn A.
Do đáy là tam tam giác đều cạnh a nên diện tích đáy là:
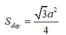
Thể tích khối chóp là:
Cho hình chóp tam giác đều S.ABC có AC = SC = 8 cm , SH = 6,93 cm ,S tam giác ABC = 27,72 cm2
a) Cho biết độ dài trung đoạn của hình chóp S.ABC.
b) Tính diện tích xung quanh và diện tích toàn phần của hình chóp S.ABC.
c) Tính thể tích của hình chóp tam giác đều S.ABC biết chiều cao của hình chóp là 7,5 cm
a) Độ dài trung đoạn của hình chóp S.ABC là độ dài đoạn thẳng từ trung điểm của cạnh đáy đến đỉnh của hình chóp. Vì tam giác ABC là tam giác đều, nên ta có thể tính độ dài trung đoạn bằng cách sử dụng công thức Pythagoras: Trung đoạn = căn bậc hai của (AC^2 - (AC/2)^2) = căn bậc hai của (8^2 - (8/2)^2) = căn bậc hai của (64 - 16) = căn bậc hai của 48 = 4 căn 3 cm
b) Diện tích xung quanh của hình chóp S.ABC là tổng diện tích các mặt bên của hình chóp. Vì tam giác ABC là tam giác đều, nên diện tích mặt bên của hình chóp là diện tích tam giác đều. Ta có công thức tính diện tích tam giác đều: Diện tích tam giác đều = (cạnh^2 * căn 3) / 4 = (8^2 * căn 3) / 4 = 16 căn 3 cm^2
Diện tích xung quanh = Diện tích tam giác đều + Diện tích đáy = 16 căn 3 + 27,72 = 16 căn 3 + 27,72 cm^2
Diện tích toàn phần của hình chóp là tổng diện tích xung quanh và diện tích đáy: Diện tích toàn phần = Diện tích xung quanh + Diện tích đáy = 16 căn 3 + 27,72 + 27,72 = 16 căn 3 + 55,44 cm^2
c) Thể tích của hình chóp tam giác đều S.ABC được tính bằng công thức: Thể tích = (Diện tích đáy * Chiều cao) / 3 = (27,72 * 7,5) / 3 = 69,3 cm^3