Cho đồ thị hàm số y = ax 4 + bx 2 + c đạt cực đại tại A 0 ; 3 và đạt cực tiểu tại B 1 ; − 3 . Tính giá trị của biểu thức P = a + 3 b + 2 c .
A. -9
B. 0
C. -24
D. -12
a, xác định parabol y = ax^2 + bx + c đạt cực tiểu bằng 4 tại x = -2 và đồ thị đi qua A ( 0 ; 6)
b, xác định GTNN của hàm số y = x^2 - 4x + 1
a.
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=-2\\4a-2b+c=4\\c=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=4a\\4a-2.4a+6=4\\c=6\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}b=4a=2\\a=\dfrac{1}{2}\\c=6\end{matrix}\right.\) \(\Rightarrow y=\dfrac{1}{2}x^2+2x+6\)
b.
\(y_{min}=y_{CT}=\dfrac{4ac-b^2}{4a}=\dfrac{4.1.1-\left(-4\right)^2}{4.1}=-3\)
Cho hàm số y = x3 + ax2 + bx + c đi qua điểm A(0;-4) và đạt cực đại tại điểm B(1;0) hệ số góc k của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ bằng -1 là:
A. k = 0
B. k = 24
C. k = -18
D. k = 18
Đáp án B
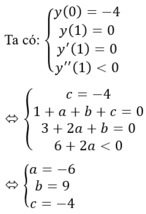
Do đó k = y’(-1) = 3 – 2a + b = 24.
Đồ thị hàm số y = a x 4 + b x 2 + c đạt cực đại tại A(0;-2) và cực tiểu tại B 1 2 ; - 17 8 . Tính a + b + c
A. a + b + c = 2
B. a + b + c = 0
C. a + b + c = -1
D. a + b + c = -3
Đáp án C.
Xét hàm số y = a x 4 + b x 2 + c , ta có y ' = 4 a x 3 + 2 b x ; y ' ' = 12 a x 2 + 2 b ; ∀ x ∈ ℝ .
Điểm A(0;-2) là điểm cực đại của đồ thị hàm số ⇒ y ' 0 = 0 ⇔ y 0 = - 2 y ' ' 0 < 0 ⇔ c = - 2 b > 0 .
Điểm B( 1 2 ; - 17 8 ) là điểm cực tiểu của đồ thị hàm số ⇒ y ' 1 2 = 0 ; y 1 2 = - 17 8 y ' ' 0 > 0
⇔ a 2 + b = 0 a 16 + b 4 + c = - 17 8 ⇔ a + 2 b = 0 a + 4 b = - 2 ⇔ a = 2 b = - 1 ⇒ a + b + c = - 1 .
Đồ thị hàm số y = ax 4 + b x 2 + c đạt cực đại tại A 0 ; − 2 và cực tiểu tại B 1 2 ; − 17 8 . Tính a + b + c
A. a + b + c = 2
B. a + b + c = 0
C. a + b + c = − 1
D. a + b + c = − 3
Đáp án C.
Xét hàm số y = a x 4 + b x 2 + c ,
ta có y ' = 4 a x 3 + 2 b x ; ∀ x ∈ ℝ .
Điểm A 0 ; − 2 là điểm cực trị đại của đồ thị hàm số ⇒ y 0 = − 2 y ' 0 = 0 ⇔ c = − 2
Điểm B 1 2 ; − 17 8 là điểm cực tiểu của đồ thị hàm số ⇒ y 1 2 = − 17 8 y ' 1 2 = 0 ⇔ a 2 + b = 0 a 16 + b 4 = − 1 8
Từ đó suy ra a = 2 ; b = − 1 ; c = − 2 ⇒ tổng a + b + c = − 1.
Cho hàm số y = e a x 2 + b x + c đạt cực trị tại x=1 và đồ thị hàm số cắt trục tung tại điểm có tung độ bằng e. Tính giá trị của hàm số tại x=2?
A. y 2 = e 2
B. y 2 = 1 e 2
C. y 2 = 1
D.. y 2 = e
Cho hàm số y = e ax 2 + bx + c đạt cực trị tại x = 1 và đồ thị hàm số cắt trục tung tại điểm có tung độ bằng e 2 . Tính giá trị của hàm số tại x = 2
A. y 2 = 0
B. y 2 = e 2
C. y 2 = 1
D. y 2 = e
Cho đồ thị hàm số y = a x 4 + b x 2 + c đạt cực đại tại A 0 ; 3 và đạt cực tiểu tại B 1 ; - 3 . Tính giá trị của biểu thức P = a + 3 b + 2 c
A. -12
B. -24
C. -9
D. 0
Đáp án B
TXĐ: D = R
Đạo hàm ![]()
Điều kiện để hàm số có cực đại và cực tiểu là ab < 0
Hàm số đạt cực đại tại A(0;3) ⇔ c = 3
Hàm số đạt cực tiểu tại 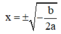 và điểm cực tiểu là B(1;-3), suy ra
và điểm cực tiểu là B(1;-3), suy ra
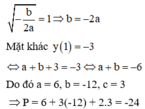
Xác định hàm số y = ax² + bx + c biết hàm đạt GTLN bằng 5 tại x = -2 và đồ thị hàm số đi qua điểm M(1; -1)
y = ax2 + bx + c đạt Max bằng 5 tại x = -2
--> a < 0; \(\dfrac{4ac - b^2}{4a}\) = 5;
\(\dfrac{-b}{2a}\) = -2
--> b = 4a; \(\dfrac{4ac - 16a^2}{4a}\) = 5
--> b = c - 5 = 4a
Đồ thị hàm số đi qua M(1; -1)
--> a + b + c = -1
--> a + 4a + 4a + 5 = -1
<=> 9a = -6
<=> a = \(\dfrac{-2}{3}\) --> b = \(\dfrac{-8}{3}\); c = \(\dfrac{7}{3}\)
--> \(y = \dfrac{-2}{3}x^2\ -\)\(\dfrac{8}{3}x\) + \(\dfrac{7}{3}\)
Cho đồ thị hàm số y = a x 4 + b x 2 + c
đạt cực đại tại A(0;3) và đạt cực tiểu tại B(1;-3). Tính giá trị của biểu thức P = a + 3b + 2c
A. -12
B. -24
C. -9
D. 0