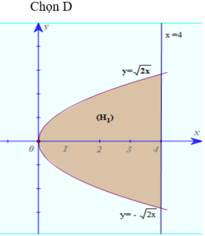
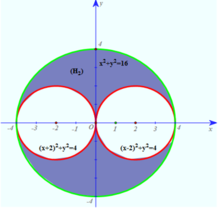
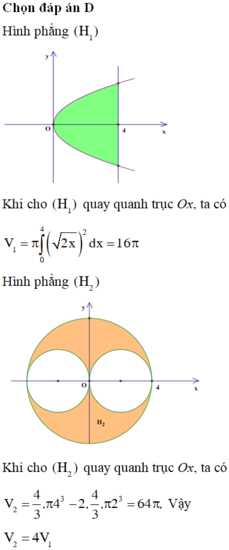
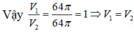Trong mặt phẳng tọa độ Oxy xét hai hình H1, H2 được xác định như sau:
H 1 = M x ; y | log 1 + x 2 + y 2 ≤ 1 + log x + y
H 2 = M x ; y | log 2 + x 2 + y 2 ≤ 2 + log x + y
Gọi S1, S2 lần lượt là diện tích của các hình H1, H2. Tính tỉ số S 1 S 2
A. 99
B. 101
C. 102
D. 100