Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và A B = a 6 2 ; A C = a 2 ; C D = a Gọi E là trung điểm của AD (tham khảo hình vẽ). Góc giữa hai đường thẳng AB và CE bằng
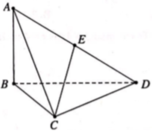
A. 60 độ
B. 45 độ
C. 30 độ
D. 90 độ
Cho tứ diện ABCD có tam giác BCD vuông tại C, AB vuông góc với mặt phẳng (BCD), AB=5a, BC=3a và CD=4a. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD.
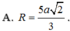
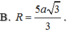
![]()
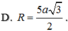
Cho tứ diện ABCD có tam giác BCD vuông tại C, AB vuông góc với mặt phẳng (BCD),
AB = 5a, BC = 3a và CD = 4a. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD .
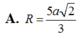
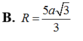
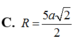
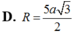
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (BCD) vuông góc với nhai. Biết tam giác ABC đêì cạnh a, tam giá BCD vuông cân tại D. Bán kính mặt cầu ngoại tiếp tứ diện ABCD bằng
A . a 2 3
B . a 3 3
C . 2 a 3 3
D . a 3 2
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và AB = a 6 2 ; AC = a 2 ; CD = a . Gọi E là trung tâm của AC (tham khảo hình vẽ bên). Góc giữa đường thẳng AB và DE bằng
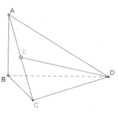
A. 45 °
B. 60 °
C. 30 °
D. 90 °
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và AB = a 6 2 , AC = a 2 , CCD = a. Gọi E là trung tâm của AC (tham khảo hình vẽ bên). Góc giữa đường thẳng AB và DE bằng
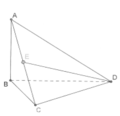
![]()
![]()
![]()
![]()
Cho tứ diện ABCD có \(\Delta\)ABC vuông tại A, AB=6 , AC=8. \(\Delta\)BCD có độ dài đường cao kẻ từ đỉnh C bằng 8. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABC). Tính góc giữa mặt phẳng (ABD) và (BCD) .
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Tan của góc giữa CM với mặt phẳng (BCD) bằng:
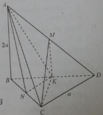
A. 2 3 3
B. 3 2
C. 2 3
D. không xác định
Cho tứ diện ABCD có tam giác BCD vuông tại B, AC vuông góc với mặt phẳng (BCD). Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD
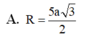
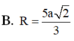
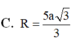

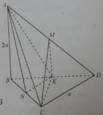
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Tan của góc giữa AC với mặt phẳng (ABD) bằng:
A. 5
B. 1
C. 51 17
D. Không xác định
Góc giữa AC với mặt phẳng (ABD) là góc KAC vì CK ⊥ (ABD) nên AK là hình chiếu của AC trên mặt phẳng (ABD).
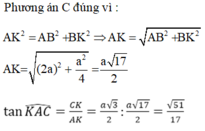
Đáp án C