Cho hàm số y = x 3 - 3 x 2 + 9 có đồ thị là (C). Điểm cực tiểu của đồ thị (C) là
A. M(0;9)
B. M(2;5)
C. M(5;2)
D. M(9;0)
PB
Những câu hỏi liên quan
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng √2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )
Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$
$\Leftrightarrow x^2-2mx+m^2-1=0$
$\Leftrightarrow x=m+1$ hoặc $x=m-1$
Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$
Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$
$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu
$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại
$BO=\sqrt{2}AO$
$\Leftrightarrow BO^2=2AO^2$
$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$
$\Leftrightarrow m=-3\pm 2\sqrt{2}$
Đúng 2
Bình luận (0)
Cho hàm số y x 3 - 3 x2 + 9 có đồ thị là (C). Điểm cực đại của đồ thị (C) là A. M (0;9) B. M (2;5) C. M (5; 2) D. M (9;0)
Đọc tiếp
Cho hàm số y = x 3 - 3 x2 + 9 có đồ thị là (C). Điểm cực đại của đồ thị (C) là
A. M (0;9)
B. M (2;5)
C. M (5; 2)
D. M (9;0)
Chọn A
Ta có:
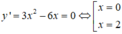
nên x = 0 là điểm cực đại của hàm số, yCĐ = 9.
Vậy điểm cực đại của đồ thị hàm số là M (0;9).
Đúng 0
Bình luận (0)
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng \(\sqrt{2}\) lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )
Xét các khẳng định sau:(I). Nếu hàm số y f(x) có giá trị cực đại là M và giá trị cực tiểu là m thì M m (II). Đồ thị hàm số
y
a
x
4
+
b
x
2
+
c
(
a
≠
0...
Đọc tiếp
Xét các khẳng định sau:
(I). Nếu hàm số y = f(x) có giá trị cực đại là M và giá trị cực tiểu là m thì M > m
(II). Đồ thị hàm số y = a x 4 + b x 2 + c ( a ≠ 0 ) luôn có ít nhất một điểm cực trị
(III). Tiếp tuyến (nếu có) tại một điểm cực trị của đồ thị hàm số luôn song song với trục hoành.
Số khẳng định đúng là :
A. 0
B. 3
C. 2
D. 1
Đáp án C
Phương pháp : Xét từng mệnh đề.
Cách giải:
(I) sai. Ví dụ hàm số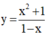 
có đồ thị hàm số như sau:
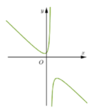õ ràng 
(II) đúng vì y ' = 4 a x 3 + 2 b x = 0 luôn có một nghiệm x = 0 nên đồ thị hàm số y = a x 4 + b x 2 + c ( a ≠ 0 ) luôn có ít nhất một điểm cực trị
(III) Gọi
x
0
là 1 điểm cực trị của hàm số 
=> Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
x
0
là: 
luôn song song với trục hoành.
Vậy (III) đúng.
Đúng 0
Bình luận (0)
Tìm m để đồ thị hàm số
y
x
4
-
2
m
+
1
x
2
+
m
có ba điểm cực trị A; B; C sao cho OA BC , trong đó O là gốc tọa độ; A là điểm cực đại, B và C là hai điểm cực tiểu của đồ thị hàm số. A.
m
2
±
2
2
B.
m
2...
Đọc tiếp
Tìm m để đồ thị hàm số y = x 4 - 2 m + 1 x 2 + m có ba điểm cực trị A; B; C sao cho OA = BC , trong đó O là gốc tọa độ; A là điểm cực đại, B và C là hai điểm cực tiểu của đồ thị hàm số.
A. m = 2 ± 2 2
B. m = 2 ± 2
C. m = 2 ± 2 3
D. m = 2 + 2 2
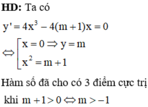
Khi đó điểm cực đại của đồ thị hàm số là A(0;m) và tọa độ 2 điểm cực tiểu là
Đúng 0
Bình luận (0)
Tìm m để đồ thị hàm số
y
x
4
-
2
m
+
1
x
2
+
m
có ba điểm cực trị A, B, C sao cho OA OB trong đó O là gốc tọa độ, A là điểm cực đại, B và C là hai điểm cực tiể...
Đọc tiếp
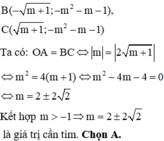
Tìm m để đồ thị hàm số y = x 4 - 2 m + 1 x 2 + m có ba điểm cực trị A, B, C sao cho OA = OB trong đó O là gốc tọa độ, A là điểm cực đại, B và C là hai điểm cực tiểu của đồ thị hàm số
A. m = 2 ± 2 2
B. m = 2 ± 2
C. m = 2 ± 2 3
D. m = 2 + 2 2
Đáp án A
Ta có: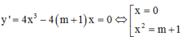 
Hàm số có 3 điểm cực trị khi m > –1
Ba điểm cực trị của đồ thị hàm số là 
; 
Đúng 0
Bình luận (0)
cho hàm số y = x 3 − 3 x 2 2 , có đồ thị là (c). gọi m là một điểm thuộc đồ thị (c). viết phương trình tiếp tuyến của ( c) tại m, biết m cùng với hai điểm cực trị của đồ thị tạo thành một tam giác có diện tích bằng 6
Cho hàm số
y
x
2
-
2
m
x
+
2
x
-
m
có đồ thị
C
m
, với m là tham số thực. Biết rằng hàm số đã cho có một điểm cực trị
x
0...
Đọc tiếp
Cho hàm số y = x 2 - 2 m x + 2 x - m có đồ thị C m , với m là tham số thực. Biết rằng hàm số đã cho có một điểm cực trị x 0 = 2 . Tìm tung độ điểm cực tiểu của đồ thị (C)
A. - 2
B. - 2 2
C. 2
D. 2 2
Cho hàm số
y
x
2
-
2
m
x
+
2
x
-
m
có đồ thị (Cm), với m là tham số thực. Biết rằng hàm số đã cho có một điểm cự...
Đọc tiếp
Cho hàm số y = x 2 - 2 m x + 2 x - m có đồ thị (Cm), với m là tham số thực. Biết rằng hàm số đã cho có một điểm cực trị x 0 = 2 Tìm tung độ điểm cực tiểu của đồ thị (C).
A.
B. 
C. 
D. 