Cho hàm số y = x 4 + a x 2 + b . Để hàm số đạt cực trị tại x = 1 và giá trị cực trị tại x = 1 bằng 3 2 thì
A. a = - 2 b = 5 2
B. a = 2 b = 5 2
C. a = - 2 b = - 5 2
D. a = 2 b = 2 5
Cho hàm số y = x 4 + a x 2 + b . Để hàm số đạt cực trị tại x = 1 và giá trị cực trị tại x = 1 bằng 3 2 thì
A. a = - 2 b = 5 2
G. a = 2 b = 5 2
C. a = - 2 b = - 5 2
D. a = 2 b = 5 2
Cho hàm số y = x 4 + a x 2 + b . Tìm a, b để hàm số đạt cực trị tại x = 1 và giá trị cực trị bằng 3 2 .
A. a = − 2 b = 5 2
B. a = 2 b = 5 2
C. a = − 2 b = − 5 2
D. a = 2 b = 2 5
Bài 1. Cho hàm số: y = 1/3 x3 - mx2 +(m2 - m + 1)x + 1. Với giá trị nào của m thì hàm số đạt cực đại tại điểm x = 1
Bài 2. Cho hàm số y = 1/3 x3 + (m2 - m + 2) x2 + (3m2 + 1)x + m - 5. Tìm m để hàm số đạt cực tiểu tại x = -2 .
Bài 3. Cho hàm số y = 1/3 x3 - (m+1) x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x = 2.
Bài 4. Tìm tất cả tham số thực m để hàm số y = (m-1)x4 - (m2 - 2) x2 + 2016 đạt cực tiểu tại
x = -1.
Bài 5. Tìm giá trị của tham số m để hàm số y = x3/3 +(2m - 1)x2 + (m - 9)x + 1 đạt cực tiểu tại
x = 2 .
Đừng hỏi tại sao tui ngu!!!
Giúp.com.vn
Cho hàm số y=f(x) có đạo hàm trên đoạn [a;b]. Ta xét các khẳng định sau:
1) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị lớn nhất của f(x) trên đoạn [a;b]
2) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị nhỏ nhất của f(x) trên đoạn [a,b]
3) Nếu hàm số f(x) đạt cực đại tại điểm x 0 và đạt cực tiểu tại điểm x 1 x 0 , x 1 ∈ a ; b thì ta luôn có f x 0 > f x 1
Số khẳng định đúng là?
A. 1
B. 2
C. 0
D. 3
Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm
x
0
∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho
x
0
∈ (a;b) và f(
x
0
)>f(x),∀x ∈ (a,b)∖{
x
0
}.
Cho hàm số y=f(x)có đạo hàm trên đoạn [a,b]. Ta xét các khẳng định sau:
1) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị lớn nhất của f(x) trên đoạn[a,b]
2) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị nhỏ nhất của f(x) trên đoạn [a,b]
3) Nếu hàm số f(x) đạt cực đại tại điểm x 0 và đạt cực tiểu tại điểm x 1 x 0 , x 1 ∈ a ; b thì ta luôn có f x 0 > f x 1
Số khẳng định đúng là?
A. 1
B. 2
C. 0
D. 3
Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm xo∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho xo∈ (a;b) và f(xo)>f(x),∀x ∈ (a,b)∖{xo}.
1,Tìm tất cả các giá trị của m để hàm số y=2x^2 - 3mx + m - 2 trên x-1 đạt cực đại tại điểm x=2. 2, Tìm tất cả các giá trị của m để hàm số y= x^2 + mx +1 trên x+m đạt cực tiểu tại điểm x=2. 3, Tìm tất cả các giá trị của m để hàm số y=x^2 -(2m-1)x+3 trên x+2 có cực đại và cực tiểu . 4, Tìm m để hso y=x^2 +m(m^2-1)x-m^4+1 trên x-m có cực đại và cực tiểu. Mọi người giúp em với ạ . Em cảm ơn ạ !
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.
Xác định m để hàm số: y = x 3 − m x 2 + (m – 2/3)x + 5 có cực trị tại x = 1. Khi đó, hàm số đạt cực tiểu hay đạt cực đại? Tính cực trị tương ứng.
Ta biết hàm số y = f(x) có cực trị khi phương trình y’ = 0 có nghiệm và y’ đổi dấu khi qua các nghiệm đó.
Ta có:
Xét y’ = 0, ta có: y′ = 3 x 2 − 2mx + (m – 2/3)
∆ ’ > 0 khi m < 1 hoặc m > 2 (∗)
Để hàm số có cực trị tại x = 1 thì
y′(1) = 3 − 2m + m – 2/3 = 0 ⇔ m = 7/3, thỏa mãn điều kiện (∗)
Với m = 7/3 thì hàm số đã cho trở thành:
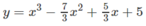
Ta có:
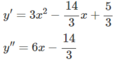
Vì y′′(1) = 6 – (14/3) > 0 nên hàm số đạt cực tiểu tại x = 1 và y CT = y(1) = (16/3).
Xác định m để hàm số: y = x 3 − m x 2 + (m – 2/3)x + 5 có cực trị tại x = 1. Khi đó, hàm số đạt cực tiểu hay đạt cực đại? Tính cực trị tương ứng.
Ta biết hàm số y = f(x) có cực trị khi phương trình y’ = 0 có nghiệm và y’ đổi dấu khi qua các nghiệm đó.
Ta có:
Xét y’ = 0, ta có: y′ = 3 x 2 − 2mx + (m – 2/3)
Δ’ > 0 khi m < 1 hoặc m > 2 (∗)
Để hàm số có cực trị tại x = 1 thì
y′(1) = 3 − 2m + m – 2/3 = 0 ⇔ m = 7/3, thỏa mãn điều kiện (∗)
Với m = 7/3 thì hàm số đã cho trở thành:
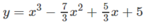
Ta có:
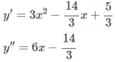
Vì y′′(1) = 6 – (14/3) > 0 nên hàm số đạt cực tiểu tại x = 1 và y C T = y(1) = (16/3).