Cho hàm số f(x) thỏa mãn f x . f ' x = 1 , với mọi x ∈ R . Biết ∫ 1 2 f x d x = a và f(1) = b, f(2) = c. Tích phân ∫ 1 2 x f x d x bằng
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số f ( x ) = 2 x + e x . Tìm một nguyên hàm F(x) của hàm số f(x) thỏa mãn F(0)=2019
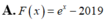
![]()
![]()
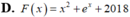
Xét các khẳng định sau
i) Nếu hàm số y = f(x) xác định trên [-1;1] thì tồn tại α ∈ - 1 ; 1 thỏa mãn f ( x ) ≥ f ( α ) ∀ x ∈ - 1 ; 1 .
ii) Nếu hàm số y = f(x) xác định trên [-1;1] thì tồn tại β ∈ - 1 ; 1 thỏa mãn f ( x ) ≤ f ( β ) ∀ x ∈ - 1 ; 1 .
iii) Nếu hàm số y = f(x) xác định trên [-1;1] thỏa mãn f(-1).f(1)<0 thì tồn tại γ ∈ - 1 ; 1 thỏa mãn f ( γ ) = 0
Số khẳng định đúng là
A. 3.
B. 2.
C. 1.
D. 0.
Cho hàm số F ( x ) = a x 3 + b x 2 + c x + 1 là một nguyên hàm của hàm số f(x) thỏa mãn f(1) = 2, f(2) = 3, f(3) = 4. Hàm số F(x) là
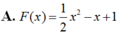
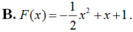
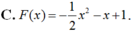
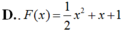
Chọn D.
Ta có
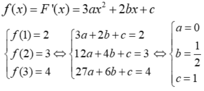
Vậy F(x)= 1 2 x 2 + x + 1
Cho hàm số y = f(x) thỏa mãn f ( 0 ) = 0 ; f ' ( x ) = x x 2 + 1 . Họ nguyên hàm của hàm số g ( x ) = 4 xf ( x ) là:
A . ( x 2 + 1 ) ln ( x 2 ) - x 2 + c
B . x 2 ln ( x 2 + 1 ) - x 2
C . ( x 2 + 1 ) ln ( x 2 + 1 ) - x 2 + c
D . ( x 2 + 1 ) ln ( x 2 + 1 ) - x 2
Cho F(x) là một nguyên hàm của hàm số f ( x ) = e x + 2 x thỏa mãn F(0)=3/2. Tìm F(x)
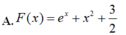
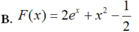
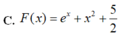
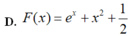
Cho hàm số f(x) thỏa mãn f'(x) + 2x f(x) = 2 xe - x 2 và f(0)=1. Tất cả các nguyên hàm của x f x e x 2 là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số f(x) có đạo hàm trên R\{0} thỏa mãn f ' ( x ) + f ( x ) x = x 2 và f(1)=1 Giá trị của f ( 3 2 ) bằng
A. 1 96
B. 1 64
C. 1 48
D. 1 24
cho hàm số f(x) thỏa mãn: (x+2)f(-x)=(1-x)f(x). Tính f(-1/2)
Cho hàm số y=f(x) thỏa mãn f(-x)=f(x). Gọi đồ thị hàm số là (C). Chọn khẳng định đúng
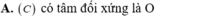
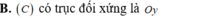
![]()
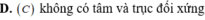
Cho hàm số f(x) thỏa mãn 2.f(1/x)+f(x)= x^2. Tính f(3)