Giúp mình cái này nữa thôi ạ, mình cảm ơn
H24
Những câu hỏi liên quan
Giúp mình cái này nữa thôi ạ
fashion
apparel
Margaretha Ley
Yes, it does
Japan
Đúng 1
Bình luận (0)
Mn ơi, tại sao mình vào HOC24 thì lại hiện lên trang LIB24 vậy ạ? Cái này mình chỉ hỏi thôi ạ!
Xin cảm ơn!!! ![]()
Vô cài đặt trang web r xóa hết dữ liệu đi, nhớ lưu mk vào r đăng nhập lại bn à:)
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
1 câu nữa thôi, mình cảm ơn nhiều ạ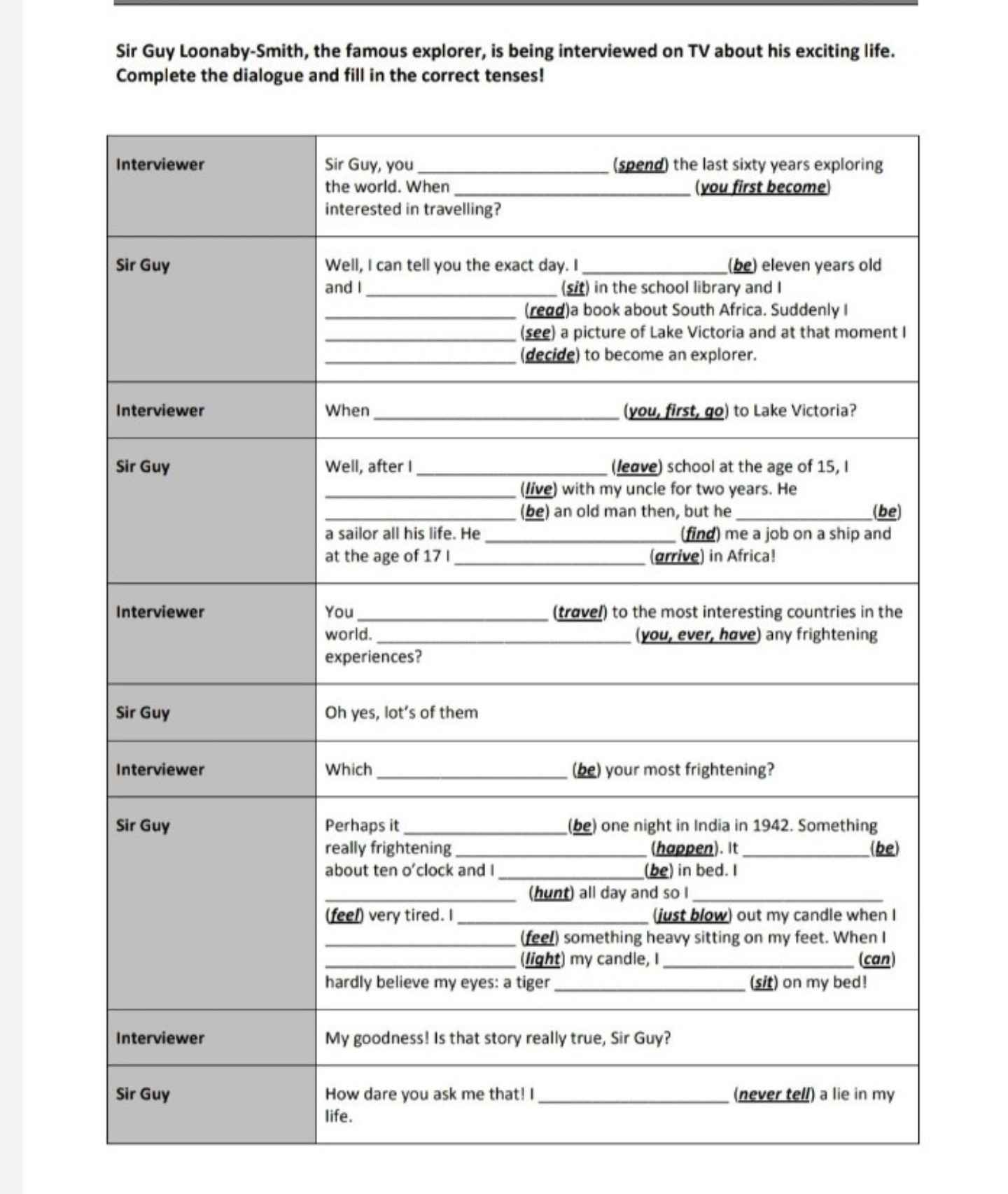
Ai đó giúp mình giải chi tiết cái này ra với ạ, mình cảm ơn nhiều
Ta có: (u.v)' = u'.v + u.v'
\(Q=80K^{\dfrac{1}{3}}\left(100-K\right)^{\dfrac{1}{2}}\)
\(Q'=80.\left(K^{\dfrac{1}{3}}\right)'.\left(100-K\right)^{\dfrac{1}{2}}+80.K^{\dfrac{1}{3}}.\left(\left(100-K\right)^{\dfrac{1}{2}}\right)'\)= \(80.\dfrac{1}{3}.K^{-\dfrac{2}{3}}.\left(100-K\right)^{\dfrac{1}{2}}+80.K^{\dfrac{1}{3}}.\dfrac{1}{2}.\left(100-K\right)^{-\dfrac{1}{2}}.\left(-1\right)\) = \(80.\left(\dfrac{\left(100-K\right)^{\dfrac{1}{2}}}{3K^{\dfrac{2}{3}}}-\dfrac{K^{\dfrac{1}{3}}}{2\left(100-K\right)^{\dfrac{1}{2}}}\right)\)= \(80.\left(\dfrac{2\left(100-K\right)^{\dfrac{1}{2}}\left(100-K\right)^{\dfrac{1}{2}}-3K^{\dfrac{2}{3}}K^{\dfrac{1}{3}}}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\right)\) = \(80.\left(\dfrac{2\left(100-K\right)-3K}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\right)\) = \(80.\left(\dfrac{200-5K}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\right)\) = \(\dfrac{400\left(40-K\right)}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\) = \(\dfrac{200\left(40-K\right)}{3K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\).
Đúng 0
Bình luận (0)
https://dembuon.vn/members/co-ko.126328/
giúp mình mn chỉ cần lên gg ghi cái này vào thôi ![]()
cảm ơn mn trc
Xem thêm câu trả lời
Bạn nào biết viết caption hay hay thì inbox mình giúp mình cái này với ạ. Cảm ơn.
làm nhanh giúp mình với mình con 1h30p nữa thôi cảm ơn

Giúp mình câu b thôi ạ! Mình cảm ơn ạ!
Đọc tiếp
Giúp mình câu b thôi ạ! Mình cảm ơn ạ!
b) Để P nguyên thì \(\sqrt{x}+5⋮3\sqrt{x}-1\)
\(\Leftrightarrow3\sqrt{x}+15⋮3\sqrt{x}-1\)
\(\Leftrightarrow16⋮3\sqrt{x}-1\)
\(\Leftrightarrow3\sqrt{x}-1\in\left\{-1;1;2;4;8;16\right\}\)
\(\Leftrightarrow3\sqrt{x}\in\left\{0;2;3;5;9;17\right\}\)
\(\Leftrightarrow3\sqrt{x}\in\left\{0;3;9\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;1;3\right\}\)
hay \(x\in\left\{0;1;9\right\}\)
Đúng 1
Bình luận (0)













