Có bao nhiêu giá trị nguyên của tham số m để phương trình
m + 3 . m + cos x 3 3 = cos x có nghiệm thực?
A. 2.
B. 7.
C. 5.
D. 3.
Có bao nhiêu giá trị nguyên của tham số m để phương trình m + 3 m + 3 cosx 3 3 = cosx có nghiệm thực
A. 5
B. 7
C. 3
D. 2
Cho phương trình log 2 2 x - 2 log 2 x - m + log 2 x = m * . Có bao nhiêu giá trị nguyên của tham số m ∈ - 2019 ; 2019 để phương trình (*) có nghiệm?
A.2021
B.2019
C.4038
D.2020
có bao nhiêu giá trị nguyên của tham số m để phương trình \(\left(m-1\right)^2x-3=4x-m\) có nghiệm dương
\(\Leftrightarrow\left(m^2-2m-3\right)x=3-m\)
\(\Leftrightarrow\left(m-3\right)\left(m+1\right)x=-\left(m-3\right)\)
- Với \(m=3\) pt vô số nghiệm
- Với \(m=-1\) pt vô nghiệm
- Với \(m\ne\left\{-1;3\right\}\) pt có nghiệm duy nhất
\(x=\dfrac{-\left(m-3\right)}{\left(m-3\right)\left(m+1\right)}=\dfrac{-1}{m+1}\)
Để pt có nghiệm dương \(\Leftrightarrow-\dfrac{1}{m+1}>0\Leftrightarrow m+1< 0\Leftrightarrow m< -1\)
Cho phương trình
5
x
+
m
=
log
5
x
-
m
với m là tham số. Có bao nhiêu giá trị nguyên của ![]() để phương trình đã cho có nghiệm?
để phương trình đã cho có nghiệm?
A. 20
B. 19
C. 9
D. 21
1. Tìm tham số m để phương trình 3cos2x-7=2m có nghiệm?
2. Trên đoạn \([0;2\pi]\) , phương trình \(2cos^2x-\sqrt{3}cosx=0\)có bao nhiêu nghiệm?
3. Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số \(y=\sqrt{2cosx-3m+14}\) xác định với mọi x thuộc R?
Help me!!!
1.
\(3cos2x-7=2m\)
\(\Leftrightarrow cos2x=\dfrac{2m-7}{3}\)
Phương trình đã cho có nghiệm khi:
\(-1\le\dfrac{2m-7}{3}\le1\)
\(\Leftrightarrow2\le m\le5\)
2.
\(2cos^2x-\sqrt{3}cosx=0\)
\(\Leftrightarrow cosx\left(2cosx-\sqrt{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\pm\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\) Có 4 nghiệm \(\dfrac{\pi}{2};\dfrac{3\pi}{2};\dfrac{\pi}{6};\dfrac{11\pi}{6}\) thuộc đoạn \(\left[0;2\pi\right]\)
Có bao nhiêu giá trị nguyên của tham số m để phương trình
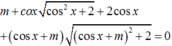
có nghiệm thực
A. 3
B. 4
C. 5
D. 6
Có bao nhiêu giá trị nguyên của tham số m để phương trình ![]() có nghiệm thực?
có nghiệm thực?
A. 9
B. 2
C. 3
D. 5
Đáp án C
Phương pháp:
Sử dụng tính đơn điệu của hàm số, đánh giá số nghiệm của phương trình.
Cách giải:
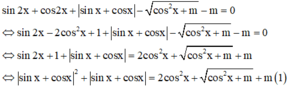
Xét hàm số ![]()
ta có ![]()
=> y = f(x) đồng biến trên khoảng ![]()
![]()
![]()
![]()
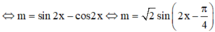 (2)
(2)
mà 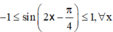
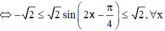
=> Để phương trình (2) có nghiệm thì ![]()
m ∈ Z => m ∈ {-1;0;1}
Vậy, có 3 giá trị nguyên của m thỏa mãn yêu cầu đề bài
Cho phương trình m . sin x + 4 cos x = 2 m − 5 với m là tham số. Có bao nhiêu giá trị nguyên của m để phương trình có nghiệm?
A. 4.
B. 7.
C. 6.
D. 5.
Đáp án C.
Áp dụng bất đẳng thức Bunhiacopxki, ta có:
m . s inx+4cosx 2 ≤ m 2 + 4 2 sin 2 x + c os 2 x = m 2 + 16.
Nên để phương trình đã cho có nghiệm ⇔ 3 m − 5 2 ≤ m 2 + 16 ⇔ 3 m 2 20 m + 9 ≤ 0.
Kết hợp với m ∈ ℤ , ta được m = 1 ; 2 ; 3 ; 4 ; 5 ; 6 là giá trị cần tìm.
Cho phương trình 2 x + m = log 2 x - m với m là tham số. Có bao nhiêu giá trị nguyên của m ∈ - 18 ; 18 để phương trình đã cho có nghiệm?
A. 19
B. 17
C. 9
D. 18